Apprentissage supervisé #
L’apprentissage supervisé fonctionne à partir de données pour lesquelles la “bonne réponse” (i.e. celle qu’on aimerait que l’algorithme fournisse systématiquement, une fois entraîné) est fournie, en tant que donnée d’entraînement. L’apprentissage supervisé correspond à la notion intuitive qu’on a de l’enseignement et de l’apprentissage : un enseignant qui pose une question à un étudiant est en mesure de le corriger en lui indiquant si sa réponse est correcte ou non (car l’enseignant connaît, à priori, la “bonne réponse” à sa propre question).
Classification #
La famille d’algorithmes d’apprentissage supervisé la plus facile à comprendre est celle des modèles de classification. Un algorithme de classification est une fonction mathématique qui associe des “objets” (donc des points dans un espace vectoriel) vers une série prédéfinie d’étiquettes, qu’on appelle souvent des “classes”.
La régression logistique #
Considérons tout d’abord un petit exemple interactif où vous jouerez vous-même
le rôle d’un modèle de classification particulier : la régression
logistique. Les données d’entraînement ont deux classes possibles : bleue ou
rouge, ainsi que deux valeurs (nombres, ou paramètres) pour les décrire :
$x$ et $y$ (puisqu’il s’agit d’un graphe en deux dimensions). La tâche du modèle
est de séparer (c-à-d classifier) les deux groupes. La ligne pointillée constitue la
“fonction de décision” du modèle : les deux classes se situent de part et
d’autre de la ligne. Comme il s’agit d’une fonction en deux dimensions, on peut
la représenter par la formule simple :
où $m$ représente la pente et $b$ l’ordonnée à l’origine. Remarquez un détail
important : il s’agit d’une fonction d’inégalité (inéquation), et non d’égalité,
ce qui veut dire qu’on peut l’interpréter en tant que fonction binaire (deux
valeurs possibles) : rouge si $f(x) \le mx + b$ et bleue si $f(x) \gt mx +
b$ (ou vice versa, arbitrairement). Quand vous déplacez cette ligne de décision
vous-même (en utilisant la souris), vous modifiez les paramètres $m$ et $b$
dynamiquement. Ces paramètres constituent le modèle. La situation idéale est
quand cette ligne de décision sépare parfaitement les points rouges des points
bleus, ce qui correspond à une valeur de 0% pour la fonction d’erreur (elle-même
représentée par la barre à droite, et distincte de la fonction de décision). Ce
n’est pas toujours possible ! Notez qu’il est possible d’ajouter ou d’enlever
des points, et de les déplacer, en utilisant la souris.
Remarquez un détail important : quoiqu’on fasse, l’erreur ne peut jamais
dépasser 50%. Quand on y pense, c’est logique, car même si on place la ligne de
décision à un endroit extrême, qui fait en sorte que TOUS les points se trouvent
d’un côté, il reste que 50% de ceux-ci sont tout de même correctement
classifiés. Et si on place la ligne dans une configuration plus pathologique,
qui ferait en sorte par exemple que 75% des points seraient incorrectement
classifiés, la chose logique à faire (ce que l’applet interactive fait en fait)
est d’inverser le schéma de classification (les points bleus deviennent
rouges, et vice versa), ce qui fait en sorte que l’erreur est réduite à 25%.
La tâche de l’algorithme de régression logistique est de trouver les “meilleures” valeurs pour les paramètres pour la fonction de décision (donc $m$ et $b$), celles qui font en sorte que la valeur de la fonction d’erreur est la plus petite possible (idéalement zéro).
Matière à réflexion : pourquoi ce n’est pas toujours possible de séparer parfaitement les points? Dans quelles conditions est-ce le cas? Qu’est-ce qui permettrait de faire en sorte que ça devienne possible?
Les mathématiques de la régression logistique (un sujet optionnel, plus complexe)
Bien que nous en ayons parlé en termes purement géométriques jusqu’ici, la
régression logistique est en fait une méthode probabiliste : un point est
considéré bleu si le modèle calcule que la probabilité qu’il le soit est $\ge
50\%$ (et évidemment vice versa pour rouge). Une probabilité est une valeur
nécessairement entre 0 et 1. Pour transformer une fonction arbitraire en une
fonction de probabilité, on peut utiliser la fonction sigmoïde (aussi appelée
fonction logistique), qui “force” une valeur à être dans la plage 0 et 1 :
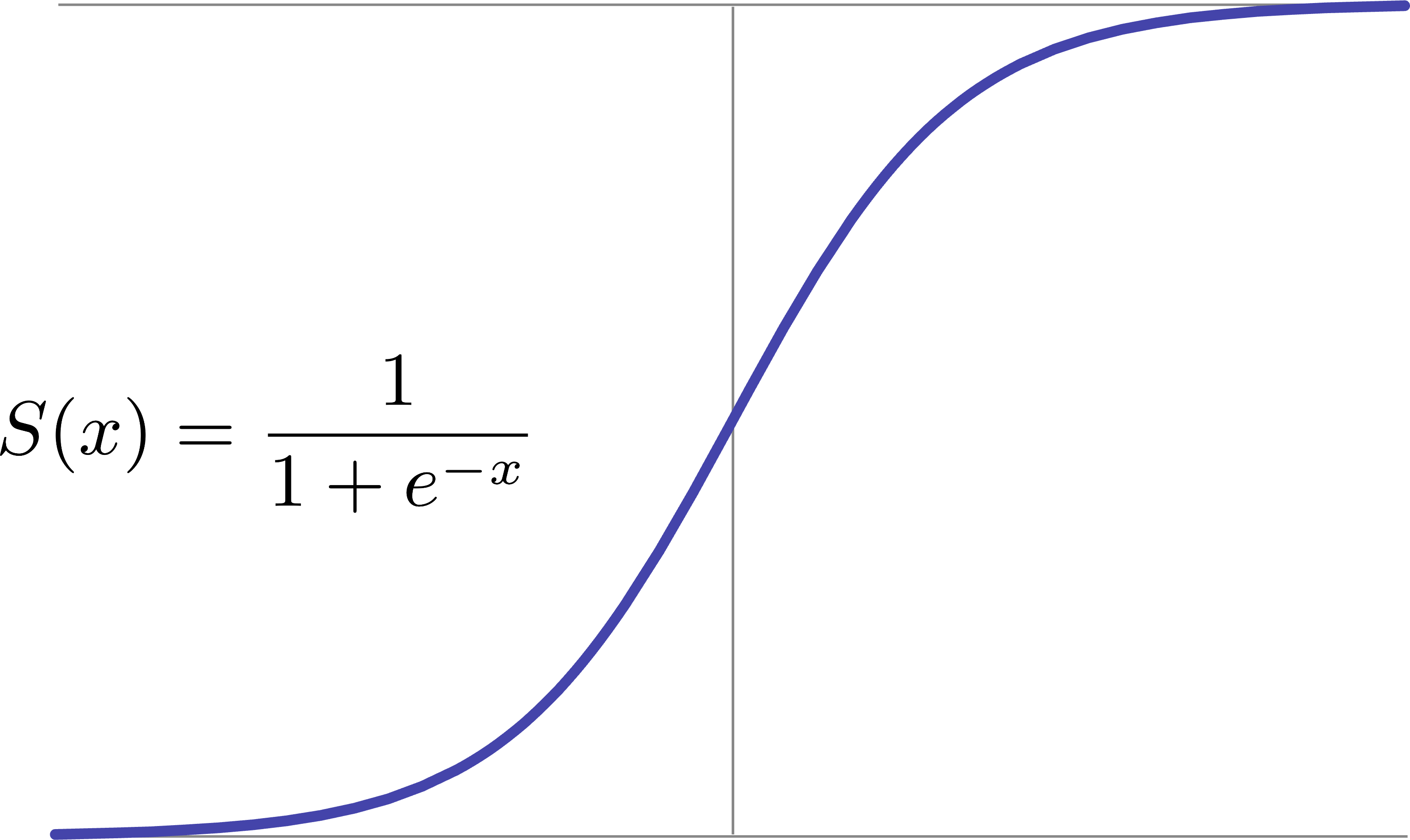
Nous allons à partir d’ici changer un peu la notation que nous avons utilisée jusqu’ici, pour la rendre plus générale :
$$\mathbf{x} = [x_1, x_2]$$$$y \in \{0, 1\}$$Cette notation classique en apprentissage automatique utilise donc $\mathbf{x}$
pour dénoter les points en 2D sous forme vectorielle ($x_1$ et $x_2$
correspondent aux $x$ et $y$ de la représentation 2D classique, et $\mathbf{x}$
est donc un vecteur, dont les 2 valeurs correspondent aux “caractéristiques”
d’un point, sa description numérique). La variable scalaire (donc une valeur
numérique simple, par opposition à un vecteur) $y$ est utilisée pour dénoter la
vraie classe d’un point (0 ou 1, correspondant arbitrairement à bleu ou
rouge). Les paramètres seront représentés par le vecteur $\mathbf{w} = [w_1,
w2]$. Il est maintenant possible de réécrire notre fonction de décision à l’aide
de cette nouvelle notation vectorielle :
($\mathbf{w}^\top \mathbf{x}$ est le produit vectoriel de $\mathbf{w}$ et $\mathbf{x}$). Notons tout d’abord qu’il y maintenant 3 paramètres ($w1$, $w2$ et $b$), alors que dans l’exemple ci-haut seulement 2 sont mentionnés : $m$ et $b$. On introduit aussi une nouvelle variable $z$ : que veut-elle dire? Pour comprendre cela, on doit faire un peu d’algèbre. Il suffit de noter que notre équation de départ :
$$y = mx + b$$est en fait équivalente à :
$$x_2 = mx_1 + b$$ce qu’on peut réécrire aisément :
$$mx_1 - x_2 + b = 0.$$En choisissant ensuite $m = -w_1/w_2$ et $b = -b/w_2$, on peut réécrire :
$$\frac{-w_1 x_1}{w_2} - x_2 - \frac{b}{w_2} = 0$$En multipliant les deux membres de l’équation par $-w_2$, on arrive à :
$$w_1 x_1 + w_2 x_2 + b = 0$$ce qui constitue la forme générale d’une équation en 2D. Étant donné que ce qui nous intéresse se passe de part et d’autre de la ligne de décision (car il s’agit comme nous l’avons vu d’une inéquation), on introduit le score $z$, pour quantifier la distance à laquelle un point se trouve, de cette ligne de séparation :
$$z = w_1 x_1 + w_2 x_2 + b$$En utilisant la fonction logistique que nous avons introduite ci-haut pour transformer ce score (une valeur arbitraire) en une probabilité (donc une valeur contrainte entre 0 et 1), on peut maintenant introduire l’équation de la régression logistique :
$$P(y) = \hat{y} = \frac{1}{1 + e^{-z}}$$avec laquelle il est bien important de comprendre que $\hat{y}$ représente une probabilité (donc que $\hat{y} \in [0, 1]$), tandis que $y$ représente une vraie classe (donc que $y \in {0, 1}$). La régression logistique transforme donc la distance entre un point et la ligne de décision, en une mesure de probabilité. L’algorithme de classification utilisera donc la probabilité calculée pour chaque point de la manière suivante :
$$ \text{classification}(x_1, x_2) = \left\{ \begin{array}{ll} \mathtt{bleu} \text{ si } \hat{y} \ge 0.5 & \\ \mathtt{rouge} \text{ si } \hat{y} < 0.5 & \\ \end{array} \right. $$Notre but est maintenant de trouver les valeurs optimales pour les paramètres $\mathbf{w}$ (donc deux nombres précis, $w_1$ et $w_2$), celles qui vont faire en sorte de minimiser l’erreur de classification. Nous avons donc besoin de définir tout d’abord cette erreur en tant que fonction précise :
$$E(y, \hat{y}) = -[y \log(\hat{y}) + (1 - y)\log(1 - \hat{y})]$$Pour bien comprendre le fonctionnement de cette équation, examinons les différents cas de figure :
- Un point est en réalité
bleu(donc $y = 1$) et la confiance du modèle en ce fait est élevée ($\hat{y} = 0.9$) : $E(y, \hat{y}) = -\log(0.9) \approx 0.1$ (l’erreur est basse). - Un point est en réalité
bleu(donc $y = 1$) mais la confiance du modèle en ce fait est basse ($\hat{y} = 0.1$) : $E(y, \hat{y}) = -\log(0.1) \approx 2.3$ (l’erreur est élevée). - Un point est en réalité
rouge(donc $y = 0$) et la confiance du modèle en ce fait est élevée ($\hat{y} = 0.1$) : $E(y, \hat{y}) = -\log(0.9) \approx 0.1$ (l’erreur est basse). - Un point est en réalité
rouge(donc $y = 0$) mais la confiance du modèle en ce fait est basse ($\hat{y} = 0.9$) : $E(y, \hat{y}) = -\log(0.1) \approx 2.3$ (l’erreur est élevée).
La fonction d’erreur $E$ que nous avons s’applique à un seul point. Nous avons besoin de la généraliser à l’ensemble des $n$ points que nous avons, en en faisant simplement la somme. Ceci est une nouvelle fonction nommée $J$, qui utilise des indices $(i)$ pour dénoter les valeurs associées aux points particuliers de notre ensemble d’entraînement :
$$J(\mathbf{w}, b) = \frac{1}{n} \sum_{i=1}^{n} E(y^{(i)}, \hat{y}^{(i)})$$$$J(\mathbf{w}, b) = \frac{1}{n} \sum_{i=1}^{n} \left[ y^{(i)} \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \log(1 - \hat{y}^{(i)}) \right]$$Vous pouvez remarquer qu’on spécifie cette fois les paramètres $\mathbf{w}$ et
$b$ pour la fonction $J$ : la raison est que nous voulons maintenant optimiser
la fonction $J$, c’est-à-dire trouver les valeurs de ses paramètres
($\mathbf{w}$ et $b$) qui vont faire en sorte de la minimiser (c-à-d que sa
valeur soit la plus petite possible, quand on considère l’ensemble de toutes ses
valeurs possibles, donc indirectement via l’ensemble de toutes les valeurs
possibles pour ses paramètres $\mathbf{w}$ et $b$). Cette opération
d’optimisation est l’essence même de l’apprentissage automatique. Apprendre,
c’est optimiser une fonction d’erreur, de manière à la rendre la plus petite
possible. On fait cela à l’aide de la technique de la descente de gradient,
qui consiste à déterminer tout d’abord la “direction” (c-à-d le vecteur) dans
laquelle la valeur de la fonction change le plus, à un point donné. Si on
utilise la métaphore d’un terrain montagneux pour représenter une fonction
d’erreur en 3 dimensions, l’altitude d’un point à un endroit particulier
représente la valeur de la fonction, tant que les coordonnées géographiques du
point (x et y, ou lat/lon si on utilise un GPS), représentent les
paramètres. Le gradient, dans cette métaphore, représente la direction dans
laquelle le changement d’altitude sera le plus abrupt.

Le symbole $\partial$ peut faire un peu peur à priori, mais sa signification devient claire quand on le traduit en mots : le gradient de la fonction $J$ par rapport au paramètre $w$ (ou $b$). Et son calcul, dans le cas de la régression logistique, est très simple : pour chaque point, on considère :
- La différence entre la probabilité produite par le modèle et la vraie étiquette : $\hat{y}^{(i)} - y^{(i)}$
- Le produit de cette différence et du vecteur d’entrée : $(\hat{y}^{(i)} - y^{(i)}) \mathbf{x}^{(i)}$ (rappelons que $\mathbf{x} = [x_1, x_2]$ est un vecteur à deux dimensions, donc ce produit sera également bi-dimensionnel, tout comme l’est également $\mathbf{w}$)
- On veut la moyenne de ces produits (donc la somme et une division)
Nos règles de mise à jour (la mise à jour, qui est un concept généralement plus associé à la programmation qu’aux mathématiques, est représentée ici par le symbole $\leftarrow$) pour les paramètres sont donc :
$$\mathbf{w} \leftarrow \mathbf{w} - \alpha \cdot \frac{\partial J}{\partial \mathbf{w}}, \quad b \leftarrow b - \alpha \cdot \frac{\partial J}{\partial b}$$L’algorithme d’optimisation (apprentissage) de la régression logistique consiste donc en l’application itérative (répétée) de ces règles de mise à jour des paramètres, qui feront en sorte de changer graduellement les valeurs de $\mathbf{w}$ et $\mathbf{b}$, tout en diminuant également progressivement la valeur de l’erreur cumulée, c’est-à-dire la valeur de la fonction $J$. $\alpha$ est le taux d’apprentissage (une simple valeur numérique), qui fait en sorte de limiter la taille des “pas” qu’on prend dans la direction du gradient, à chaque itération. Pour le distinguer des paramètres ($\mathbf{w}$ et $\mathbf{b}$), on appelle $\alpha$ un hyper-paramètre.
La programmation de la régression logistique (un sujet optionnel, plus technique)
Si cela vous intéresse, voici du code Python qui met en oeuvre la régression logistique que nous venons d’étudier. Le code est délibérément détaillé et assez “bas niveau”, car il utilise seulement numpy, une librairie pour faire des opérations basées sur l’algèbre linéaire (ainsi que Matplotlib pour faire les visualisations). Si on utilisait une librairie d’apprentissage automatique spécialisée, comme Scikit-learn par exemple, le code serait plus simple et compact, étant donné que le niveau d’abstraction serait plus élevé (bien qu’il s’agirait toujours de Python, le code serait de plus “haut niveau”). Il n’est pas nécessaire de comprendre ce code dans les détails, mais il peut s’avérer intéressant d’en avoir un aperçu, car il est très représentatif de ce qui se fait dans de vrais environnements de programmation.
Classification bayésienne naive (gaussienne) #
Examinons maintenant un autre algorithme de classification que nous pourrions utiliser sur nos données en deux dimensions.
La régression logistique est un algorithme d’apprentissage discriminatif :
elle tente de modéliser la probabilité qu’un exemple appartienne directement à
une classe (bleue ou rouge) directement à partir des caractéristiques de cet
exemples ($x_1$ et $x_2$). En contraste, la classification naive bayésienne est
un algorithme génératif, qui tente tout d’abord de modéliser la distribution
statistiques des classes, avant d’utiliser ces modèles (un modèle pour la classe
bleue et un pour la classe rouge) pour déterminer si un point particulier a
plus de chance d’avoir été généré par un modèle particulier (disons rouge)
plutôt qu’un autre. Cette “inversion” qui permet à un modèle discriminatif d’être construit
en fonction d’un modèle génératif sous-jacent, est effectuée à l’aide d’un résultat fondamental
en probabilité : le théorème de Bayes.
Les mathématiques de la classification bayésienne naive (optionnel)
Chaque couple dimension + classe sera modélisé par une gaussienne à une
dimension (donc 4 modèles en tout : un pour la classe rouge sur la dimension
$x$, un pour la classe bleue aussi sur $x_1$, et la même chose pour la
dimension $x_2$). Une gaussienne (aussi appelée distribution normale) est la
fameuse “courbe en cloche”, qui détermine comment la “masse de probabilité” est
répartie autour d’une valeur centrale (qu’on appelle la moyenne) :
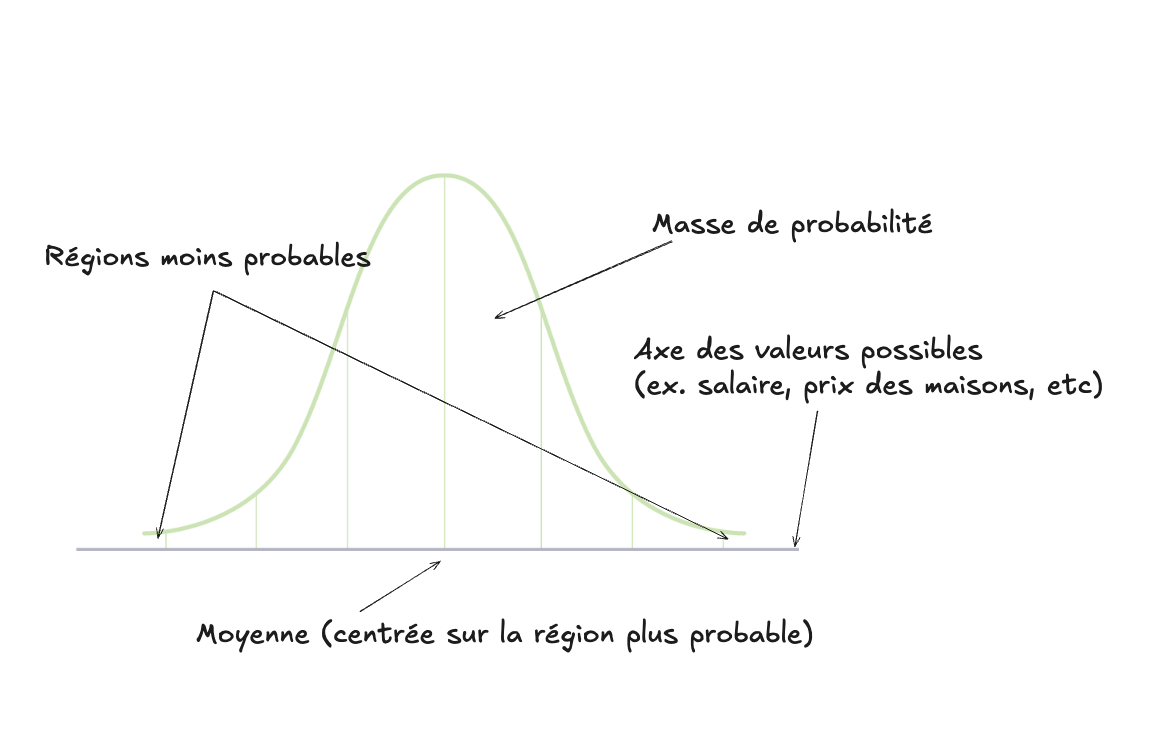
La gaussienne est une fonction continue 1D car elle n’a qu’une seule valeur dépendante (l’axe horizontal). L’axe vertical, la valeur de la fonction, correspond à la masse de la probabilité. Remarquez un aspect important : la valeur de la fonction à un point précis donné sur l’axe horizontal (par exemple la moyenne) ne correspond PAS à la probabilité de ce point, malgré ce que l’intuition voudrait croire. Étant donné que la masse de probabilité est une fonction continue, pour obtenir une probabilité donnée il faut calculer l’intégrale de la fonction entre deux points donnés. Étant donné que la totalité de la masse (l’aire sous la courbe) est 1, on peut dire que la probabilité qu’un événement soit plus petit que la moyenne (ou plus grand) est de 50% (c-à-d que l’aire sous la courbe, ou l’intégrale, de la partie à droite ou à gauche de la barre verticale de la moyenne totalise 0.5).
Mais donc que veut-on dire par la modélisation par une gaussienne?
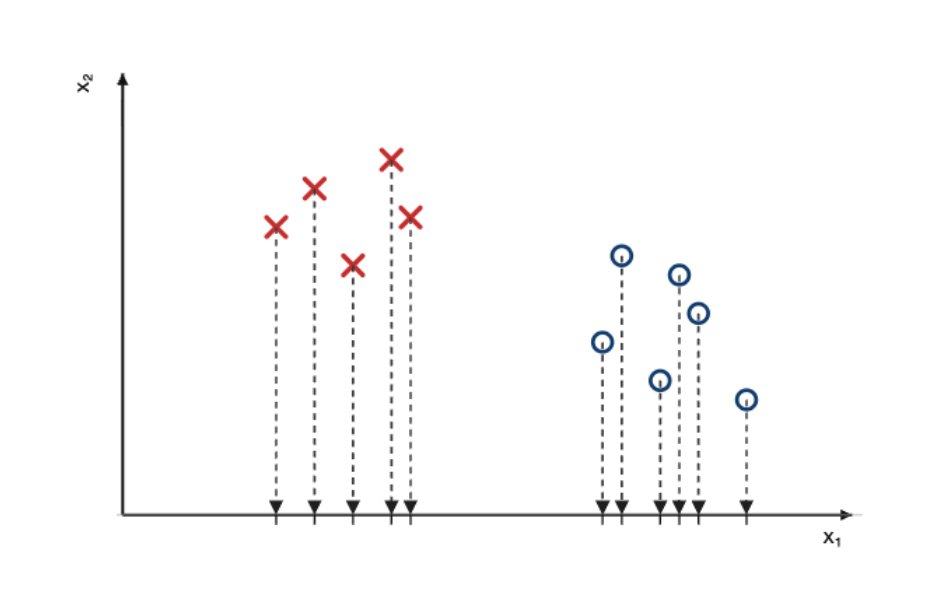
La première étape consiste à projeter les points sur l’axe $x_1$, ce qui les rend uni-dimensionnels.
Une fois les points projetés, on peut modéliser (c-à-d décrire mathématiquement) les classes de points à l’aide de gaussiennes, dont l’épaisseur correspondra à la densité (ou quantité) de points projetés sur l’axe, pour chaque classe.
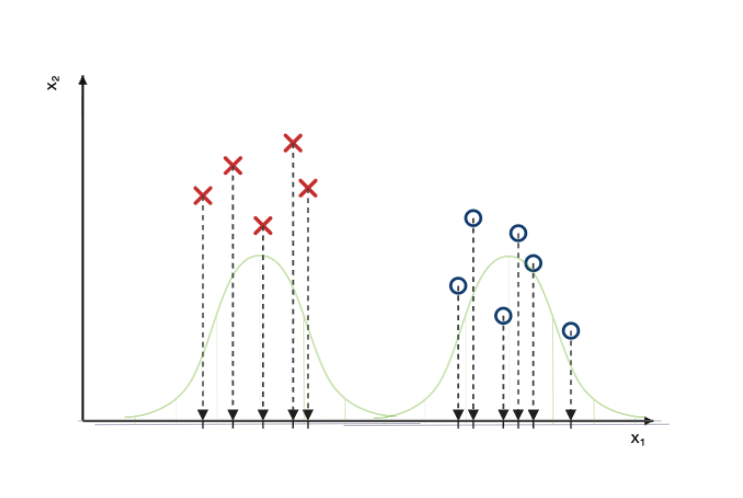
On répète la procédure pour les deux classes, sur l’axe $x_2$.
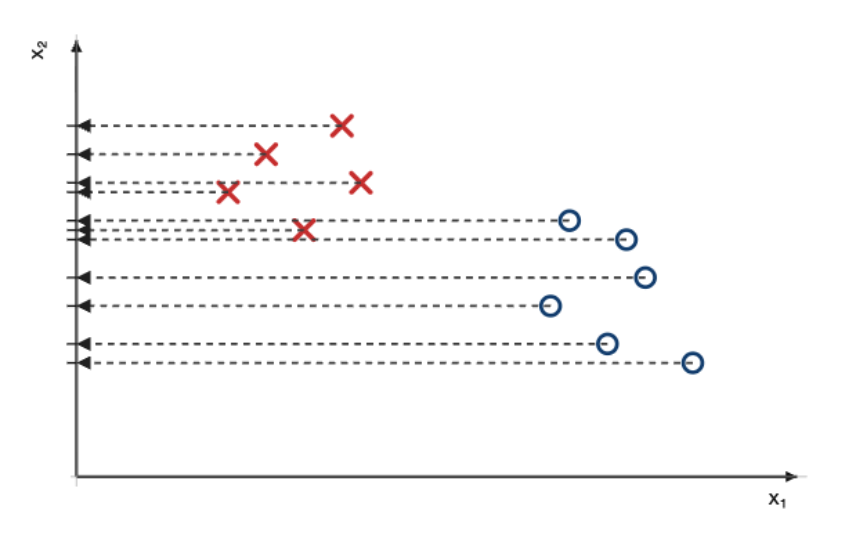
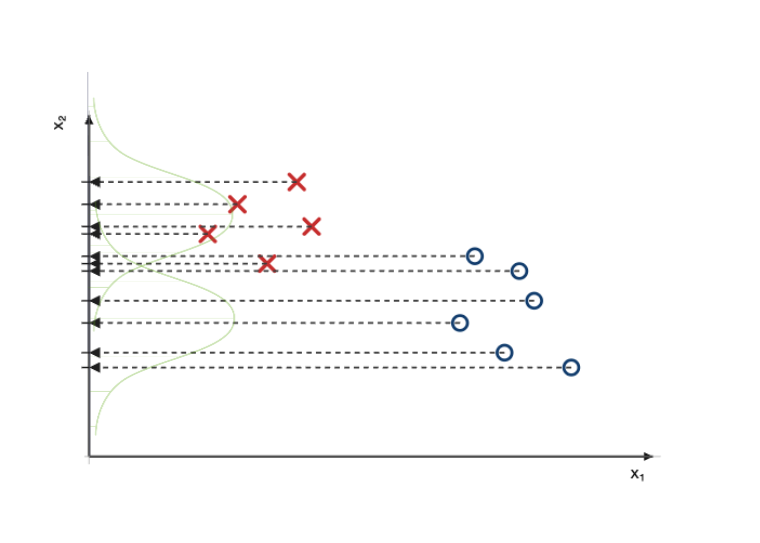
À ce stade, nous avons donc quatre modèles :
$$p(x_1 \mid \text{rouge}) = \mathcal{N}(x_1; \mu_{1,\text{rouge}}, \sigma_{1,\text{rouge}}^2)$$$$p(x_2 \mid \text{rouge}) = \mathcal{N}(x_2; \mu_{2,\text{rouge}}, \sigma_{2,\text{rouge}}^2)$$$$p(x_1 \mid \text{bleue}) = \mathcal{N}(x_1; \mu_{1,\text{bleue}}, \sigma_{1,\text{bleue}}^2)$$$$p(x_2 \mid \text{bleue}) = \mathcal{N}(x_2; \mu_{2,\text{bleue}}, \sigma_{2,\text{bleue}}^2)$$où $\mathcal{N}$ représente la gaussienne, et $\mu$ et $\sigma$ représentent ses paramètres (qui déterminent sa forme particulière). L’apprentissage d’un modèle de classification naive bayésienne constitue donc le calcul des valeurs optimales pour ces différents paramètres, que l’on peut faire directement dans ce contexte (en contraste de la méthode itérative que nous avons utilisée pour l’apprentissage des paramètres de la régression logistique) :
$$\hat\mu_{1,\text{rouge}}=\frac{1}{N_{\text{rouge}}}\sum_{i\in I_{\text{rouge}}} x_{i1},\quad$$$$\hat\mu_{2,\text{rouge}}=\frac{1}{N_{\text{rouge}}}\sum_{i\in I_{\text{rouge}}} x_{i2},$$$$\hat\mu_{1,\text{bleue}}=\frac{1}{N_{\text{bleue}}}\sum_{i\in I_{\text{bleue}}} x_{i1},\quad$$$$\hat\mu_{2,\text{bleue}}=\frac{1}{N_{\text{bleue}}}\sum_{i\in I_{\text{bleue}}} x_{i2},$$$$\hat\sigma^2_{1,\text{rouge}}=\frac{1}{N_{\text{rouge}}}\sum_{i\in I_{\text{rouge}}}(x_{i1}-\hat\mu_{1,\text{rouge}})^2,\quad$$$$\hat\sigma^2_{2,\text{rouge}}=\frac{1}{N_{\text{rouge}}}\sum_{i\in I_{\text{rouge}}}(x_{i2}-\hat\mu_{2,\text{rouge}})^2,$$$$\hat\sigma^2_{1,\text{bleue}}=\frac{1}{N_{\text{bleue}}}\sum_{i\in I_{\text{bleue}}}(x_{i1}-\hat\mu_{1,\text{bleue}})^2,\quad$$$$\hat\sigma^2_{2,\text{bleue}}=\frac{1}{N_{\text{bleue}}}\sum_{i\in I_{\text{bleue}}}(x_{i2}-\hat\mu_{2,\text{bleue}})^2.$$On peut combiner les modèles :
$$p(x_1, x_2 \mid \text{rouge}) \;=\; p(x_1 \mid \text{rouge}) \cdot p(x_2 \mid \text{rouge})$$$$p(x_1, x_2 \mid \text{bleue}) \;=\; p(x_1 \mid \text{bleue}) \cdot p(x_2 \mid \text{bleue})$$ou encore, pour simplifier :
$$P(\mathbf{x} \mid y)$$Notez qu’on change ici la notation de $p$ à $P$, pour mettre l’emphase sur le
fait que nous passons d’une fonction de densité à une fonction de probabilité.
Ce modèle est génératif, car il génère un point $\mathbf{x}$ (donc ses
coordonnées $x_1$ et $x_2$), à partir d’une classe donnée $y$ (rouge ou
bleue). On dit aussi que ce que ce modèle est la probabilité de $\mathbf{x}$
conditionnelle à $y$.
Mais ce qui nous intéresse, dans un contexte de classification, est l’équivalent de ce que nous avons calculé pour le modèle de régression logistique, soit :
$$P(y \mid \mathbf{x})$$Il semble donc que notre modèle génératif soit le contraire de ce qu’on l’on veut. Est-il possible de “l’inverser”, pour obtenir le modèle que l’on souhaite, soit la probabilité d’une classe étant donné un point?
Il est possible de faire cela à l’aide du théorème de Bayes (ce qui explique donc le nom de l’algorithme), qui stipule que :
$$P(y \mid \mathbf{x}) \;=\; \frac{P(\mathbf{x} \mid y) \, P(y)}{P(\mathbf{x})}$$Nous connaissons déjà évidemment $P(\mathbf{x} \mid y)$, que nous avons calculé
ci-haut, et $P(y)$ est simple à calculer : il s’agit simplement de la
probabilité à priori (sans aucune autre connaissance) que les points soient
rouges ou bleus (ce qui est possiblement 50%, équiprobable, si notre
ensemble d’entraînement est balancé, moitié rouge moitié bleu).
$P(\mathbf{x})$ est moins clair (la probabilité à priori des données?), mais
étant donné que cette valeur ne dépend pas de $y$, on peut simplement l’ignorer
pour obtenir un algorithme de classification final :
Tout comme la régression logistique que nous avons étudiée, cet algorithme produit une décision linéaire, pour des raisons mathématiques que nous n’allons pas explorer plus à fond.
Question intéressante à se poser : pourquoi la décision est une ligne?
Classification bayésienne naive (multinomiale) #
Nous avons vu jusqu’à présent deux exemples de classificateurs supervisés en deux dimensions : la régression logistique et le naïf bayésien gaussien. Ces modèles travaillaient directement dans l’espace des variables réelles, où chaque donnée est représentée par un point dans le plan.
Nous allons maintenant changer de domaine d’application et considérer un problème plus concret : la détection de courriels indésirables (pourriels, ou spam en anglais). Ce sera aussi le sujet de votre travail noté 2.
Représenter un courriel comme un vecteur #
Comme nous l’avons expliqué dans le chapitre sur les données, un texte peut être représenté par un vecteur dans l’« espace des mots ». Dans ce modèle vectoriel, chaque dimension correspond à un mot du vocabulaire, et la valeur dans cette dimension correspond au nombre de fois que le mot apparaît dans le document.
Ainsi, un courriel devient un vecteur en très haute dimension :
$$\mathbf{x} = (n_{1}, n_{2}, \ldots, n_{V})$$où $n_{i}$ est le nombre d’occurrences du mot $i$ dans le courriel, et $V$ est la taille du vocabulaire.
Il est utile de faire l’effort de se représenter l’analogie entre le $\mathbf{x}$ de nos exemples 2D précédents, et ce $\mathbf{x}$ qui vit dans un espace de beaucoup plus grande dimension, et composé de valeurs entières au lieu de valeurs continues (les comptes pour chaque dimension / mot), mais tout de même un vecteur de même nature.
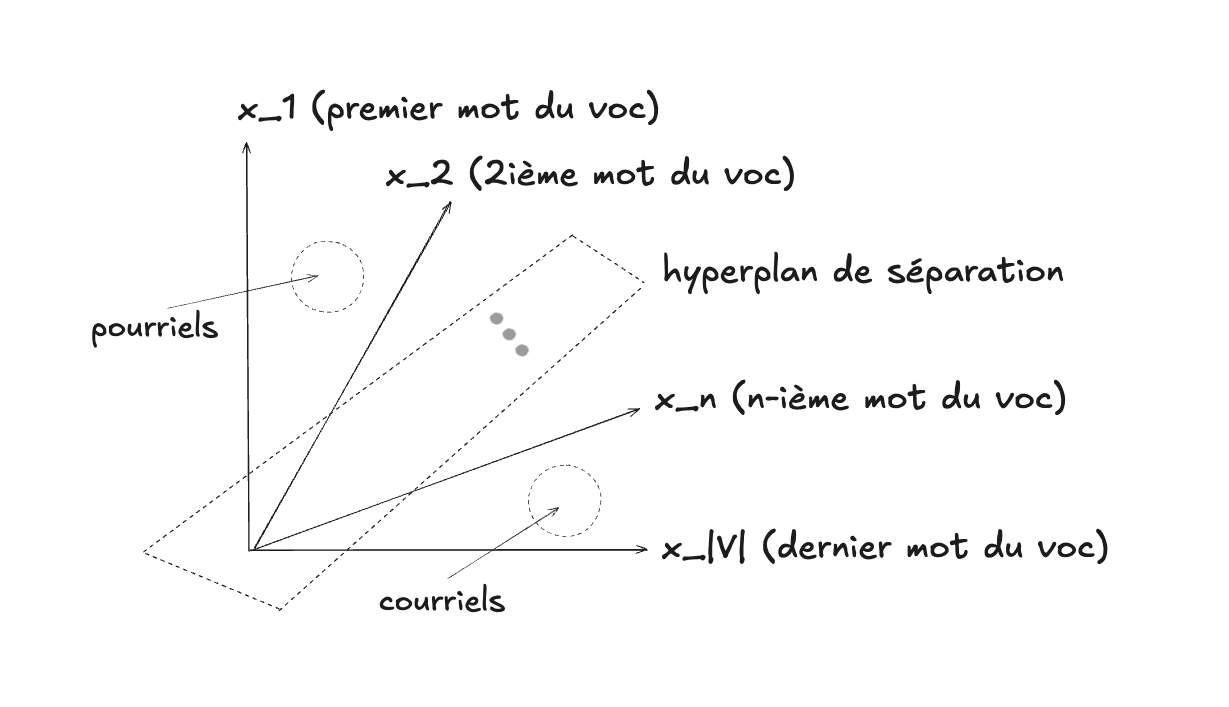
Les mathématiques de la classification naive multinomiale (optionnel)
Le modèle probabiliste : multinomial #
Dans le cas du classificateur naïf bayésien pour les données en deux dimensions,
nous avions supposé que chaque classe (par exemple bleu et rouge) était
associée à une distribution gaussienne. Autrement dit, nous modélisions la
distribution des variables continues $x_1$ et $x_2$ à l’aide d’une loi normale.
Ce modèle est génératif dans le sens où il génère les données d’une classe
(vecteurs 2D pour les classes bleu ou rouge, et vecteurs en dimension $|V|$
pour les classes pourriel ou courriel).
Dans le cas du texte d’un courriel, la situation est différente. Les variables $n_i$ sont des comptes de mots, et il est naturel de les modéliser par une distribution multinomiale. Si on lance un dé à 6 faces 1000 fois, la distribution multinomiale permet de calculer la probabilité d’obtenir $X_1$ fois la face, $X_2$ fois la face 2, et ainsi de suite. Il s’agit donc d’une distribution qui modélise des événements discrets (des comptes entiers) par opposition à la distribution normale qui modélise des valeurs continues.
Si un courriel appartient à la classe pourriel, alors la probabilité
d’observer un vecteur $\mathbf{x}$ de comptes de mots est :
où :
- $N = \sum_{i=1}^{V} n_i$ est le nombre total de mots du courriel,
- $p_i$ est la probabilité à priori qu’un mot de classe
pourrielsoit le mot $i$ (cette probabilité à priori est probablement plus grande pour le mot “prix” que pour le mot “parent”, par exemple).
De la même façon, on définit un modèle multinomial pour la classe courriel.
Rappel : hypothèse de naïveté #
Comme dans le modèle gaussien naïf bayésien, nous faisons l’hypothèse que les mots sont générés indépendamment les uns des autres. Cette hypothèse est évidemment fausse (certains mots apparaissent souvent ensemble), mais elle rend le modèle beaucoup plus simple et efficace en pratique.
Décision du classificateur #
Pour classer un courriel, nous utilisons la règle de Bayes :
$$P(\text{pourriel} \mid \mathbf{x}) = \frac{P(x \mid \text{pourriel}) \, P(\text{pourriel})}{P(\mathbf{x})}$$$$P(\text{courriel} \mid \mathbf{x}) = \frac{P(\mathbf{x} \mid \text{courriel}) \, P(\text{courriel})}{P(\mathbf{x})}$$ce qui permet, en ignorant $P(\mathbf{x})$ pour la même raison que celle expliquée ci-haut, d’obtenir un algorithme de classification similaire à celui que nous avons déjà vu :
$$ \text{classification}(\mathbf{x}) = \left\{ \begin{array}{ll} \mathtt{pourriel} \text{ si } P(\mathbf{x} \mid \text{pourriel}) P(\text{pourriel}) \ge P(\mathbf{x} \mid \text{courriel}) P(\text{courriel}) & \\ \mathtt{courriel} \text{ sinon } & \\ \end{array} \right. $$Cela montre que la décision finale est une combinaison linéaire pondérée des fréquences de mots, ce qui fait le lien avec la régression logistique étudiée précédemment.
Autres algorithmes de classification #
Le monde des algorithmes de classification supervisé est extrêmement riche et créatif, et il en existe de très nombreux exemples, dont les principes et modes de fonctionnement sont complètement différents de ce que nous avons vu (paramétriques, non-paramétriques, inductifs, etc.). Parmi les plus connus, on retrouve :
Régression #
Comme nous l’avons vu, les algorithmes de classification permettent de trouver les paramètres optimaux d’une fonction qui détermine à quelle classe, ou étiquette, un exemple appartient (par ex. est-ce que cette image est un chat ou un chien, est-ce que ceci est un pourriel ou un courriel?). Nous avons expliqué également en quoi il s’agit d’apprentissage automatique supervisé, car l’entraînement se fait à l’aide de la “bonne” étiquette (ou classe), qu’on connaît, qui est donnée à priori.
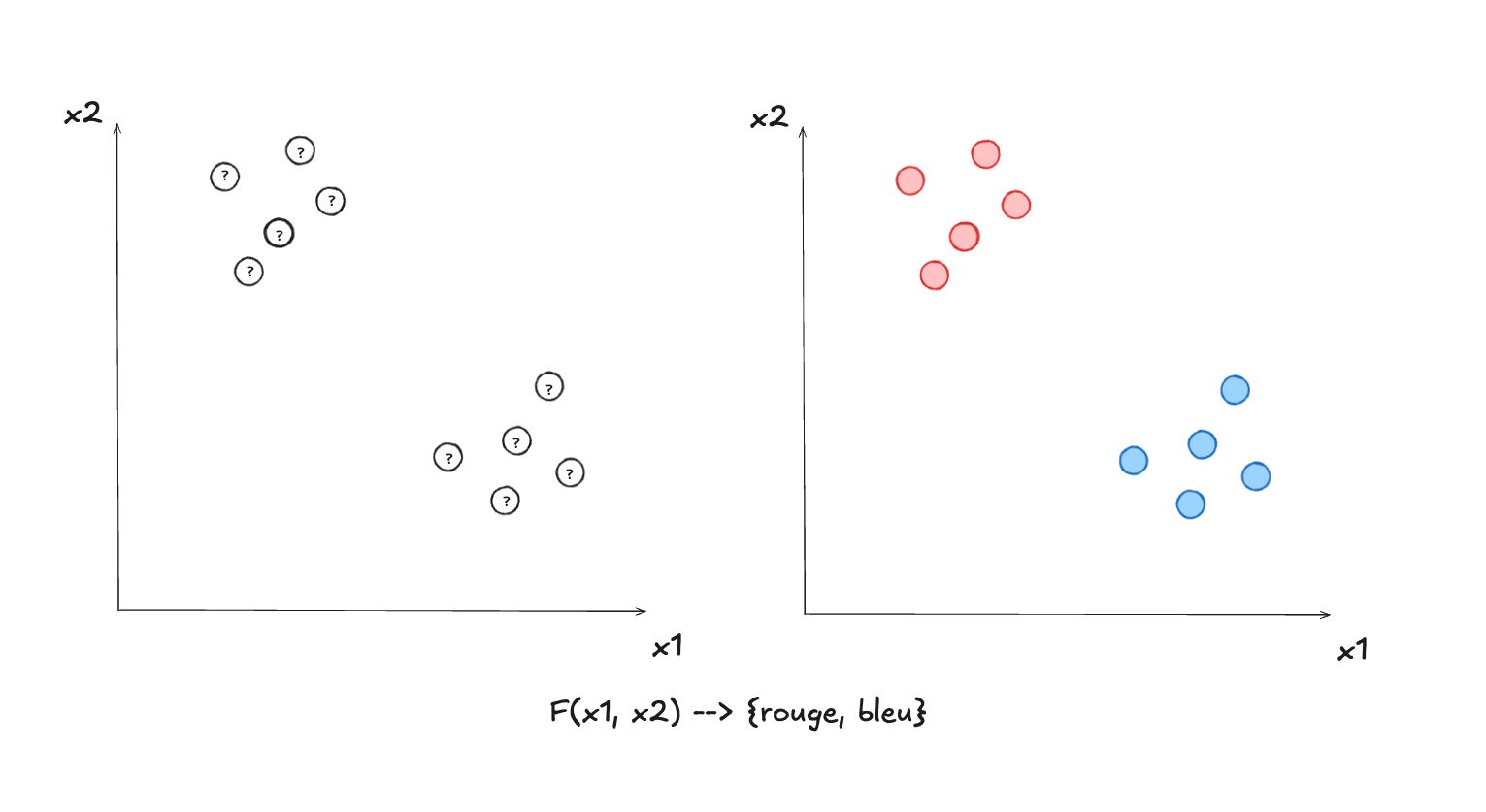
Nous allons voir maintenant que les régressions sont une autre famille d’algorithmes d’apprentissage supervisé où on cherche plutôt à trouver les paramètres optimaux d’une fonction au sens général, qui va fournir une valeur distincte pour chaque exemple. Par exemple, je pourrais vouloir avoir une fonction qui me fournit l’estimé du prix d’une maison, à partir de ses dimensions, de son année de construction et de son lieu géographique. Ou encore, une fonction pour estimer le temps de vol, à partir du lieu de départ, la destination, et la grosseur de l’avion utilisé.
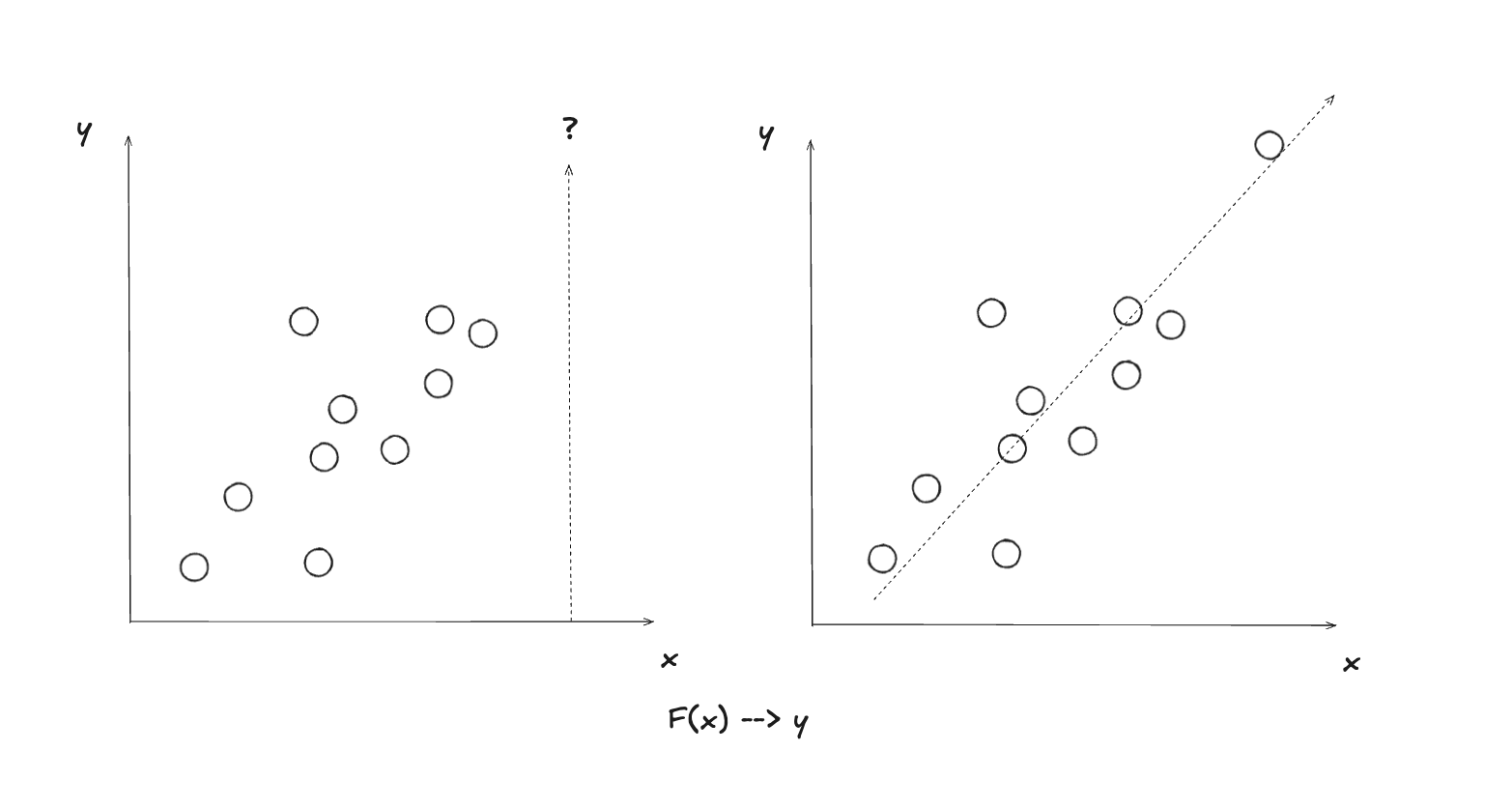
Une fonction de classification a un nombre restreint de valeurs possibles, tandis qu’une fonction de régression a une infinité de valeurs possibles. Dans les deux cas il s’agit d’apprentissage supervisé, car dans les deux cas, on possède la “bonne réponse” (soit sous la forme d’une catégorie connue d’avance, ou de valeur d’une fonction connue d’avance) pour faire l’entraînement du modèle, c’est-à-dire trouver les paramètres optimaux, ceux qui font en sorte de minimiser l’erreur de classification ou de régression.
Attention à la confusion possible avec le fait que la régression logistique est un algorithme de classification, en dépit de son nom.
Régression linéaire #
Il existe de nombreux algorithmes de régression, mais nous allons nous contenter d’étudier le plus simple et le plus classique : la régression linéaire. Il s’agit d’un algorithme particulièrement vénérable en fait, qui a des origines historiques profondes, qui datent de bien avant l’informatique moderne.
Les gens sont souvent un peu surpris et même incrédules d’apprendre que la modeste régression linéaire est une forme d’intelligence artificielle… Ils se demandent quel peut bien être le rapport entre trouver les coefficients d’une fonction linéaire et ChatGPT? C’est bel et bien le cas pourtant, et ceci illustre bien le fait qu’il y a des liens profonds entre les statistiques (le domaine auquel la régression linéaire est classiquement associé) et l’IA au sens moderne (qui est surtout centrée sur l’apprentissage automatique, qui est une forme de statistiques sur les stéroïdes, qui combine la puissance des mathématiques et des ordinateurs modernes).
Voici tout d’abord un petit exemple interactif de régression linéaire, pour vous faire une idée intuitive de son fonctionnement. Les points sont tout d’abord distribués de manière semi-aléatoire, c’est à dire qu’ils suivent grossièrement la forme d’une fonction linéaire implicite, dont les paramètres exacts sont connus de l’applet interactive, mais non de vous. Votre tâche est d’ajuster la fonction (donc ses paramètres) de manière à minimiser la fonction d’erreur. Notez que la fonction de séparation ne peut être que linéaire, c’est une contrainte fondamentale de cet algorithme, qui évidemment explique aussi son nom.
Comme vous avez pu le constater dans l’exemple interactif ci-dessus, la régression linéaire vise à trouver la ligne droite qui “colle” le mieux à un ensemble de points dispersés. Contrairement à la classification, où l’on sépare des groupes en catégories discrètes (comme bleu ou rouge), ici on cherche à prédire une valeur continue pour chaque point d’entrée. Imaginez que les points représentent des maisons : l’axe x pourrait être la superficie en mètres carrés, et l’axe y le prix de vente. La ligne que vous ajustez deviendrait alors une fonction qui estime le prix d’une maison en fonction de sa taille – une prédiction numérique précise, plutôt qu’une simple étiquette. Le principe de base est simple : on suppose que la relation entre les variables est linéaire, c’est-à-dire qu’elle peut être décrite par l’équation classique d’une droite :
$$y = mx + b$$où :
- $y$ est la valeur prédite (par exemple, le prix de la maison),
- $x$ est la variable d’entrée (par exemple, la superficie),
- $m$ est la pente (qui indique comment $y$ change quand $x$ augmente),
- $b$ est l’ordonnée à l’origine (la valeur de $y$ quand $x = 0$).
Bien sûr, dans la réalité, les données ne tombent pas parfaitement sur une ligne droite – il y a du bruit, des variations imprévues. C’est là que la notion d’erreur entre en jeu : l’algorithme mesure à quel point la ligne prédite s’éloigne des points réels, et ajuste $m$ et $b$ pour minimiser cette erreur globale.
Matière à réflexion : pourquoi assume-t-on une relation linéaire ? Dans quels cas cela pourrait-il ne pas suffire, et que faire alors ? (Indice : pensez à des extensions comme la régression polynomiale.)
La fonction d’erreur : mesurer l’imperfection #
Pour quantifier “à quel point c’est mauvais”, on utilise une fonction d’erreur (aussi appelée fonction de perte ou de coût). Dans la régression linéaire, la plus courante est l’erreur quadratique moyenne (Mean Squared Error, ou MSE en anglais). Pour chaque point de données, on calcule la différence entre la valeur réelle $y_i$ et la valeur prédite $\hat{y}_i = m x_i + b$, on met cette différence au carré (pour éviter que les erreurs positives et négatives s’annulent, et pour pénaliser plus les grosses erreurs), puis on fait la moyenne sur tous les points.
Géométriquement, la régression linéaire cherche la droite qui minimise la somme des distances verticales (et non perpendiculaires) entre chaque point et la ligne. Ces distances verticales correspondent exactement aux résidus dont nous parlions. Si vous imaginez que chaque point est relié à la ligne par un ressort vertical, la position d’équilibre de la ligne correspondrait exactement à la solution de la régression linéaire. Vous développerez probablement une meilleure intuition pour ce processus en manipulant l’application interactive suivante :
Les mathématiques de la régression linéaire (optionnel)
Mathématiquement, pour $n$ points de données :
$$J(m, b) = \frac{1}{n} \sum_{i=1}^{n} (y_i - (m x_i + b))^2$$Cette fonction $J$ est comme une “carte topographique” de l’erreur : pour chaque paire de valeurs $(m, b)$, elle donne une hauteur représentant le niveau d’erreur. L’objectif est de trouver le point le plus bas de cette carte – les valeurs optimales de $m$ et $b$ qui minimisent $J$. Dans l’exemple interactif, quand vous déplacez la ligne avec la souris, vous modifiez $m$ et $b$ manuellement, et vous voyez l’erreur diminuer (ou augmenter) en temps réel. Mais un algorithme fait ça automatiquement, de manière systématique.
Minimiser l’erreur : deux approches principales #
Il existe deux façons classiques de trouver ces paramètres optimaux : une méthode analytique (exacte et rapide pour des cas simples) et une méthode itérative (plus générale, surtout utile pour des problèmes complexes ou en haute dimension).
1. La méthode des moindres carrés (analytique) #
C’est la plus traditionnelle, inventée par Gauss au 19e siècle. L’idée est de résoudre directement l’équation qui met les dérivées partielles de $J$ à zéro (les points où la pente de la “carte topographique” est nulle, donc un minimum). Pour notre cas simple en une dimension :
$$ \frac{\partial J}{\partial m} = 0 \quad \text{et} \quad \frac{\partial J}{\partial b} = 0 $$En résolvant ces équations, on obtient des formules fermées pour $m$ et $b$ :
- $ m = \frac{n \sum (x_i y_i) - \sum x_i \sum y_i}{n \sum x_i^2 - (\sum x_i)^2} $
- $ b = \frac{\sum y_i - m \sum x_i}{n} $
C’est comme appuyer sur un bouton “calculer” : pas d’itérations, juste un résultat exact. Ça marche super bien pour des données pas trop volumineuses, et c’est ce que font la plupart des tableurs comme Excel quand vous ajoutez une “tendance linéaire” à un graphique.
2. La descente de gradient (itérative) #
C’est la même technique que nous avons vue pour la régression logistique ! On imagine $J(m, b)$ comme une vallée montagneuse en 3D (avec $m$ et $b$ comme coordonnées x et y, et l’erreur comme altitude). On commence avec des valeurs aléatoires pour $m$ et $b$, puis on calcule le gradient (la direction de la pente la plus raide vers le bas) et on fait un petit pas dans cette direction. On répète jusqu’à ce que l’erreur ne diminue plus beaucoup.
Les règles de mise à jour sont :
$$ m \leftarrow m - \alpha \cdot \frac{\partial J}{\partial m} $$$$ b \leftarrow b - \alpha \cdot \frac{\partial J}{\partial b} $$Où $\alpha$ est le taux d’apprentissage (un hyper-paramètre que l’on ajuste : trop grand, et on risque de “sauter” par-dessus le minimum ; trop petit, et ça prend une éternité). Les dérivées partielles sont :
$$ \frac{\partial J}{\partial m} = -\frac{2}{n} \sum_{i=1}^{n} x_i (y_i - (m x_i + b)) $$$$ \frac{\partial J}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (m x_i + b)) $$Cette méthode est puissante car elle s’étend facilement à plus de dimensions (par exemple, prédire le prix d’une maison avec superficie, âge, et nombre de chambres – on aurait alors $y = w_1 x_1 + w_2 x_2 + w_3 x_3 + b$, avec un vecteur de poids $\mathbf{w}$). C’est aussi la base de l’entraînement des réseaux de neurones modernes.
Une fois qu’on a fait des efforts pour comprendre le fonctionnement de certains algorithmes de base en apprentissage automatique, il peut être intéressant de considérer, à nouveau, notre question d’ordre philosophique (ou linguistique) : en quoi, au juste, est-ce que cela constitue de l’intelligence, artificielle ou non? Nous allons voir par la suite en quoi les idées relativement simples et peu puissantes que nous avons développées dans ce module vont évoluer vers les systèmes beaucoup plus impressionnants qui jouent un rôle de plus en plus important dans notre vie moderne.