Que sont les données, et comment les représenter?#
Il y a une tension fondamentale en informatique entre les différentes manières de représenter les données, et ce qu’elles peuvent signifier. Quand on ajoute l’apprentissage automatique, la situation devient encore plus complexe. Tentons de clarifier le tout.
Niveau des bits, physiques et mathématiques#
Au niveau le plus fondamental, l’ordinateur, physiquement et logiquement, ne
peut traiter qu’un seul type de donnée : le bit, qui est à la fois un concept
mathématique (un symbole dont la valeur ne peut être que 0 ou 1 généralement, ou
vrai ou faux plus spécifiquement en logique) et physique, au niveau de
l’implémentation, soit en terme électrique (mémoire RAM, CPU, disque SSD), de
magnétisme (disque dur) ou de caractéristiques optiques (CD). Les bits
représentent les nombres via la convention de l’encodage binaire.
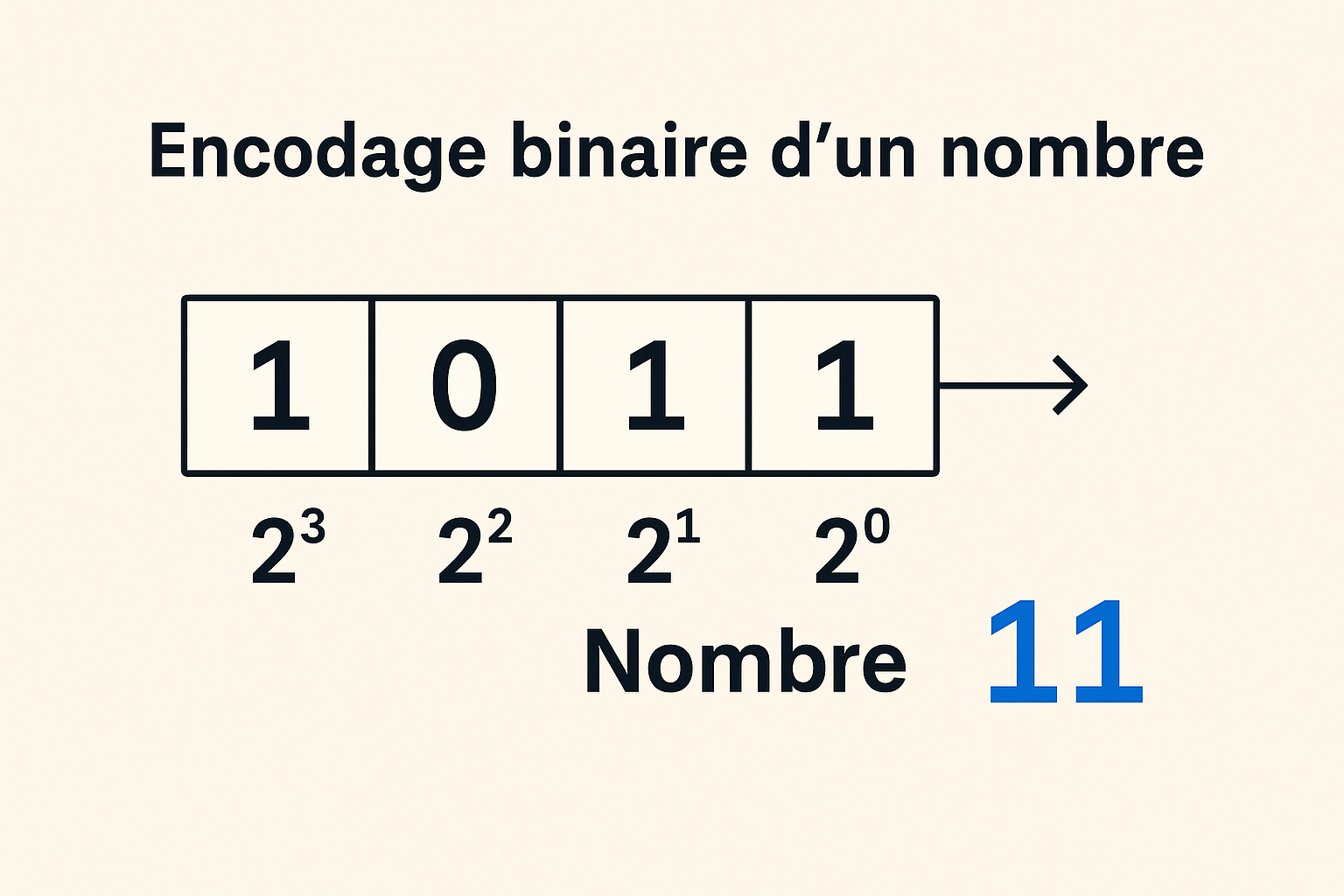
Niveau de l’ordinateur et de son langage#
Au niveau suivant, on trouve l’ordinateur lui-même, dont le mécanisme central est le microprocesseur (CPU). Un CPU traite les bits sous leur forme physique, et il interprète des “paquets” (ou mots) de bits de taille déterminée (souvent 32, 64 ou 128 bits) de deux manière fondamentalement différentes :
- En tant que nombre (ou plus généralement valeur)
- En tant qu’instruction
Le flot de bits auquel est exposé le CPU (soit via sa mémoire physique, ou via un autre médium physique comme un disque) constitue un programme, et le CPU exécute ce programme, de manière séquentielle et dynamique. Un programme dans un “langage machine” (le langage du CPU) fictif pourrait être par exemple :
MOV 1000
ADD 0001
STR 2000Les symboles MOV, ADD et STR sont des instructions, qui correspondent en fait
elles-mêmes à des nombres (donc des séries de bits). En réalité, le CPU verrait peut-être
la séquence suivante :
1000 1000
1001 0001
1002 2000si MOV, ADD et STR correspondaient par convention aux valeurs 1000, 1001
et 1002. La signification de ce programme pourrait être la suivante :
- Prendre la valeur à l'adresse mémoire 1000 et la mettre dans un registre
- Ajouter 1 à cette valeur dans le registre
- Prendre le contenu du registre et l'enregistrer à l'adresse mémoire 2000Comment le CPU peut-il distinguer entre 1000 en tant qu’instruction MOV, ou
1000 en tant que valeur? Une manière simple serait de simplement respecter la
convention selon laquelle les “paquets de bits” (de taille fixe) aux positions
paires (dans la séquence du programme) sont des instructions, tandis que ceux
aux positions impaires sont des valeurs (dans la réalité c’est un peu plus
complexe, mais l’idée est semblable, il s’agit de conventions préétablies). Et
qu’est-ce que le CPU doit “faire” pour exécuter une instruction particulière? Il
s’agit en fait d’un mini-programme (pour cette instruction particulière) qui est
implémenté directement dans les circuits du CPU. C’est l’endroit où la logique
et la matière se touchent !
Vous pouvez exécuter vous-même pas à pas une version interactive de ce mini-programme :
Niveau de la programmation symbolique#
Le prochain niveau est implémenté en terme du langage du niveau précédent : tout comme il est possible d’écrire un jeu, un système d’exploitation ou tout autre type de programme dans le langage natif du CPU (le langage machine), il est également possible d’écrire.. un autre langage ! Cet autre langage sera en général plus abstrait (plus éloigné donc de la réalité physique de l’ordinateur), ce qui permettra au programmeur d’exprimer des idées computationnelles plus complexes, d’une manière plus naturelle et expressive (C++, Python ou JavaScript sont des exemples de langage de cette catégorie). Pour mieux comprendre la notion d’un langage en tant que programme, on peut imaginer qu’il s’agit d’une sorte “d’ordinateur virtuel”, implémenté en terme d’un langage moins abstrait (le langage machine). Ce langage de “plus haut niveau” (plus abstrait) doit encore une fois traiter avec des instructions et des valeurs (toujours, ultimement, représentées en termes de bits), mais cette fois on voit apparaître des représentations plus complexes, pouvant encoder des structures plus riches et diverses :
- des nombres entiers
- des nombres réels (beaucoup plus complexe à représenter!)
- des chaînes de caractères (strings)
- des listes de nombres
- des listes de mots
- des listes de listes de mots
- des images
- des sons
- etc!
Niveau de l’apprentissage automatique et des mathématiques#
L’aspect “algorithmique” d’un algorithme d’apprentissage automatique réfère au fait qu’on effectue en général une procédure, une séquence d’opérations (ou de transformations) sur des données qui sont essentiellement de nature numérique. Cette procédure est généralement écrite dans un langage du niveau précédent, par exemple Python. L’aspect mathématique des algorithmes d’apprentissage automatique exige des structures des données et des représentations plus sophistiquées et performantes. L’outil conceptuel le plus souvent utilisé pour les données d’AA est l’espace vectoriel, souvent de très haute dimensionnalité (bien au-delà des trois dimensions dans lesquelles nous vivons quotidiennement).
Prenons l’exemple de l’image d’une maison. Il est raisonnable à priori de considérer qu’une image est représentée dans un espace à deux dimensions, la grille 2D de ses pixels :
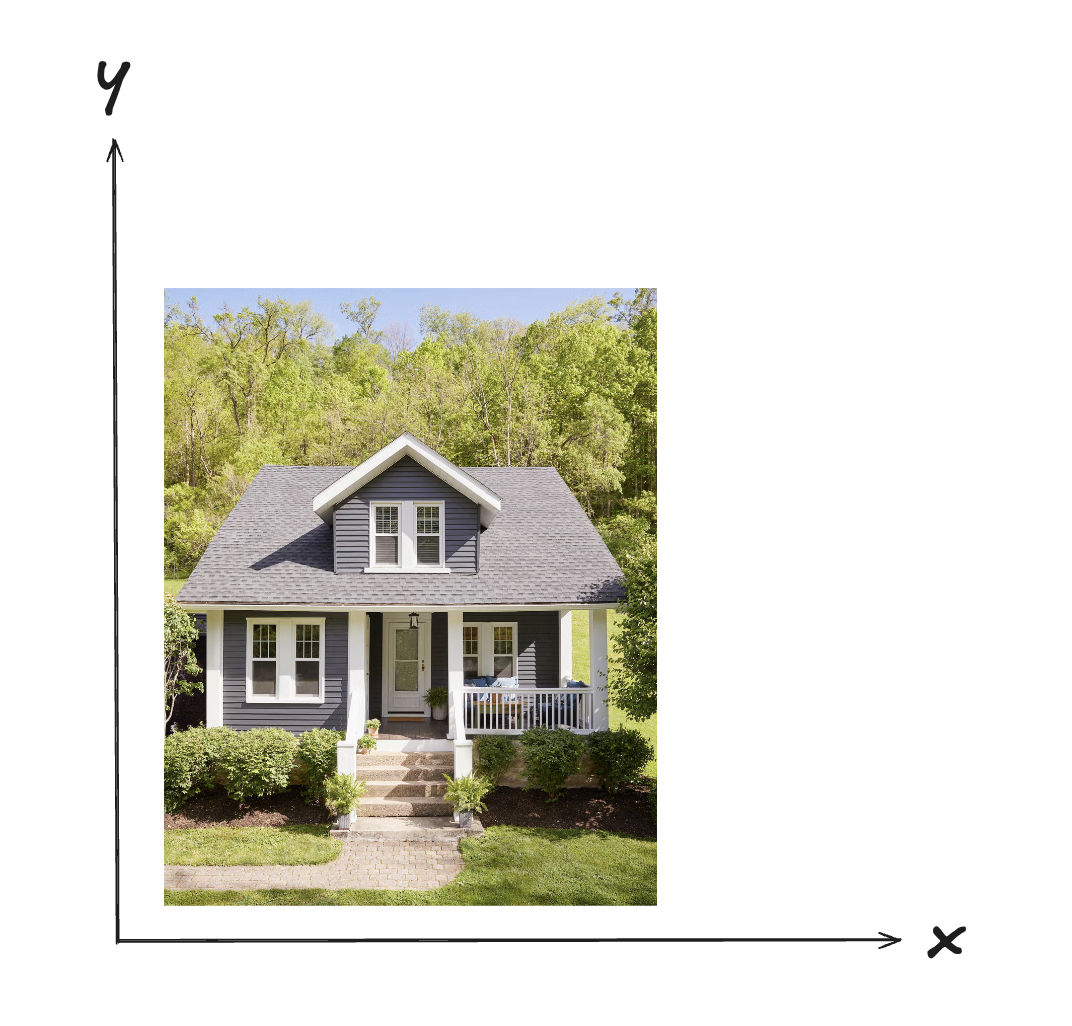
Pourtant, s’il s’agissait d’une maison dans un jeu vidéo, elle pourrait être représentée par un modèle vectoriel en trois dimensions (ce qui permettrait de rendre l’environnement dynamique, avec une caméra, à l’aide d’algèbre linéaire) :
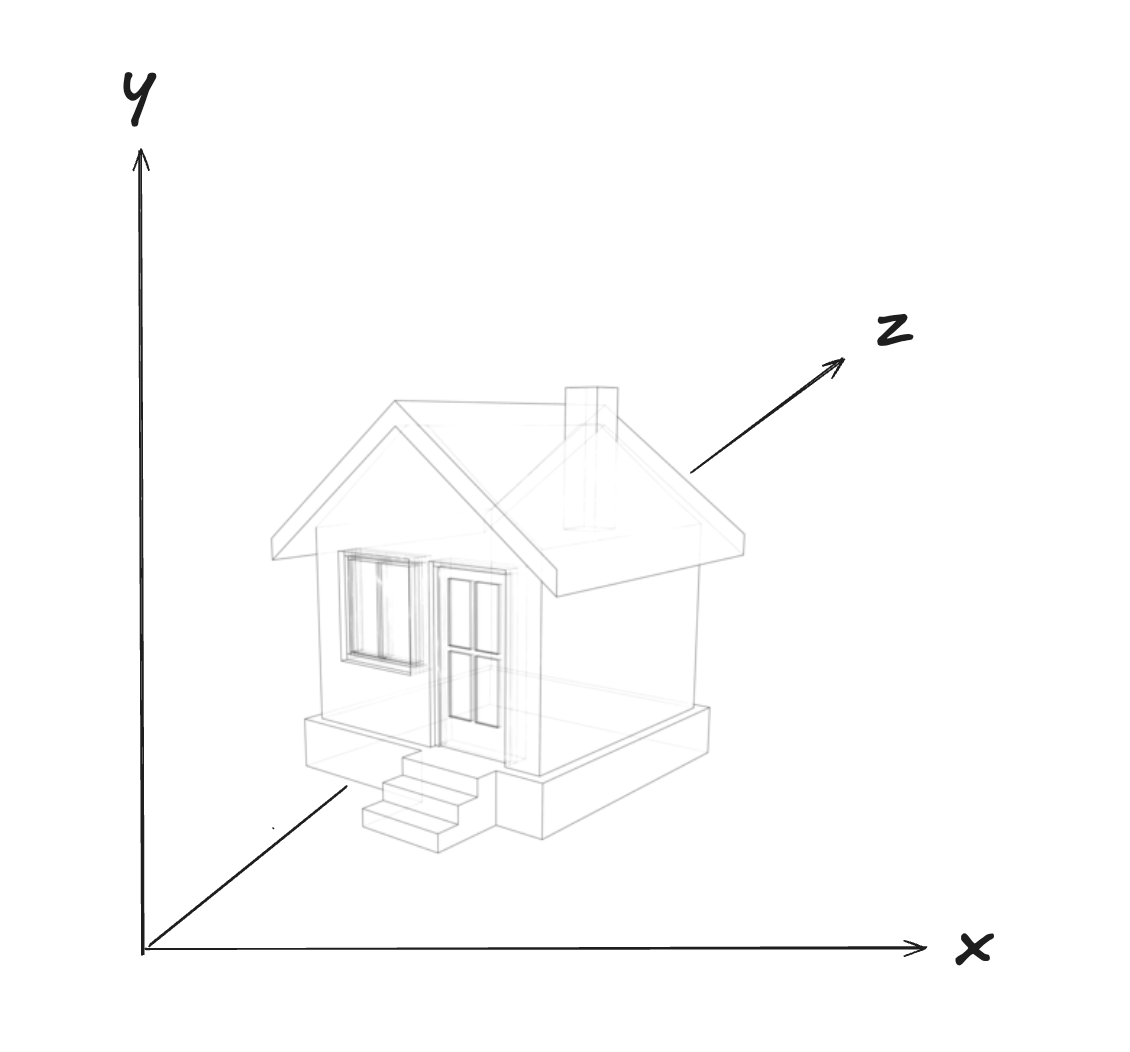
Mais dans le contexte de l’apprentissage automatique, nous allons en fait considérer un espace beaucoup plus difficile à imaginer et représenter, un espace multi-dimensionnel avec lequel il y a autant de dimensions que de pixels :
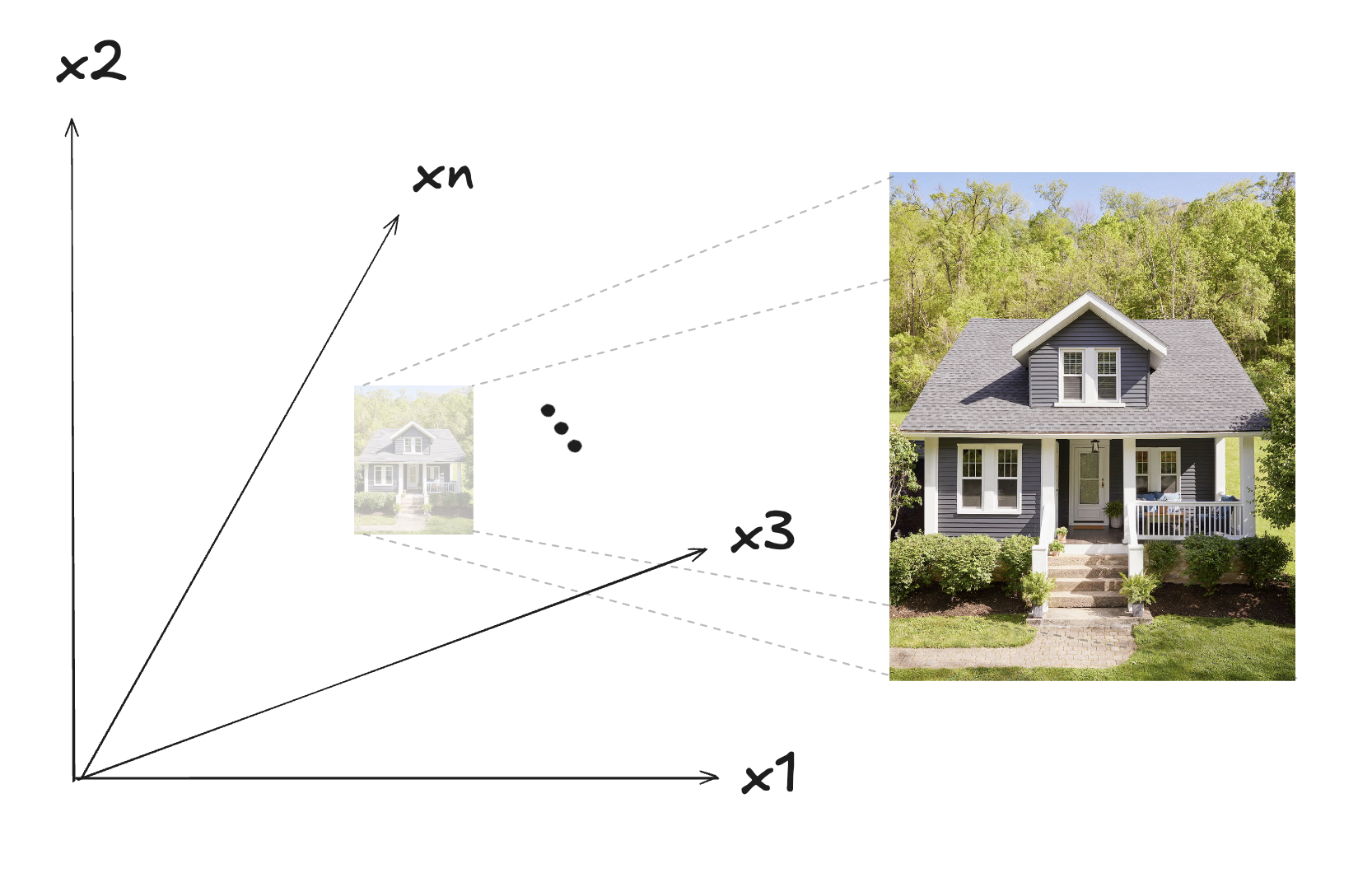
Si notre image a 1000 X 2000 pixels par exemple, il s’agira donc d’un espace à 6,000,000 dimensions (1000 x 2000 x 3 couleurs de base pour chaque pixel : rouge, bleu et vert). Il s’agit d’un espace absolument énorme, qu’il n’est pas possible de se représenter visuellement. Un “point” dans cet espace représente une image entière et particulière, correspondant aux valeurs de sa position relative à chacune des 6,000,000 dimensions. Si on ne modifie qu’un seul pixel de cette image, il s’agira en fait d’un autre point (donc une autre image), proche, mais tout de même différent du premier.
Les images ne sont utilisées qu’avec certains types d’algorithmes d’apprentissage, mais l’idée générale de l’espace vectoriel à plusieurs dimensions, pour représenter des objets ou des concepts, est très importante et répandue. On pourrait utiliser un tel espace pour représenter les caractéristiques quantitatives (features) d’une maison :
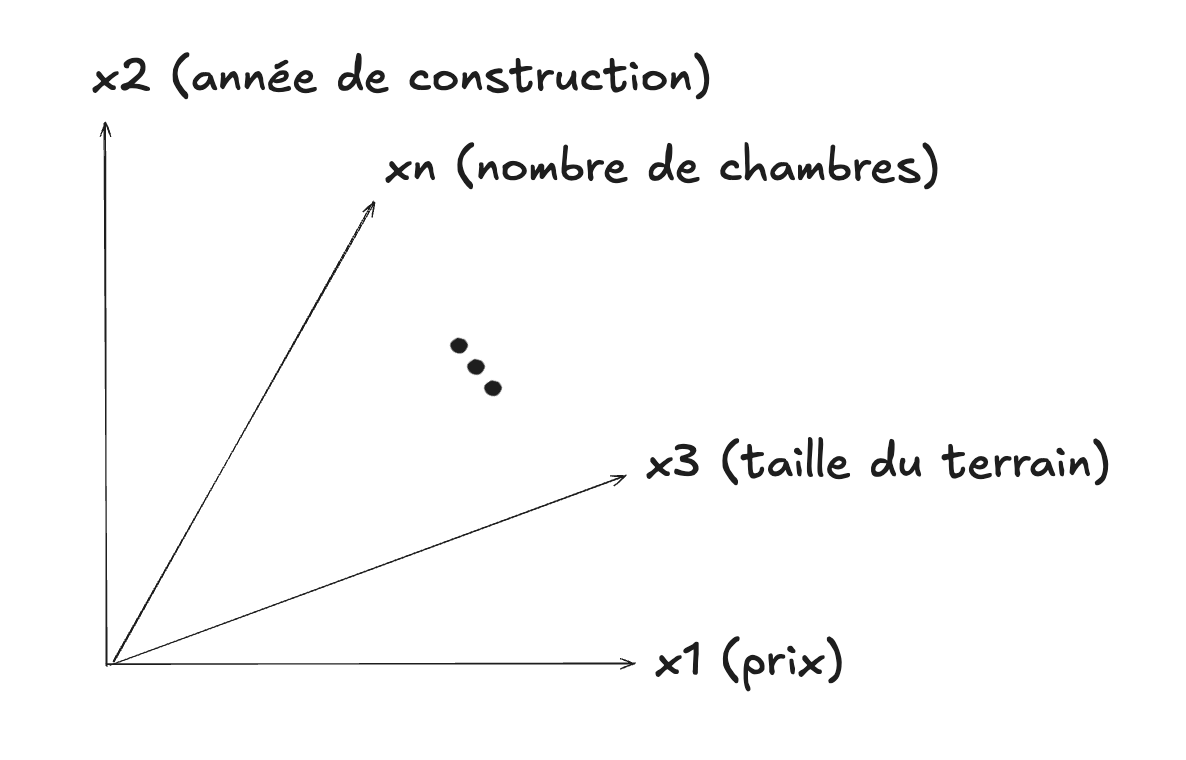
Un tel espace pourrait servir à représenter des données tabulaires de ce genre par exemple :
| x1 (prix) | x2 (année de construction) | x3 (taille du terrain, m²) | x4 (surface habitable, m²) | x5 (nombre de chambres) | x6 (nombre de salles de bain) |
|---|---|---|---|---|---|
| 420 000 | 1995 | 600 | 180 | 4 | 2 |
| 350 000 | 1980 | 500 | 150 | 3 | 1 |
| 580 000 | 2010 | 720 | 220 | 5 | 3 |
| 310 000 | 1972 | 450 | 130 | 3 | 1 |
| 760 000 | 2020 | 850 | 260 | 6 | 3 |
| 490 000 | 2005 | 640 | 200 | 4 | 2 |
| 270 000 | 1965 | 400 | 110 | 2 | 1 |
| 690 000 | 2018 | 780 | 240 | 5 | 2 |
| 330 000 | 1988 | 520 | 145 | 3 | 1 |
| 815 000 | 2022 | 900 | 280 | 6 | 4 |
Donc même s’il s’agit d’un tableau à deux dimensions, les données qu’il contient sont multidimensionnelles.
Les GPUs#
Il serait possible d’implémenter un espace vectoriel entièrement avec les primitives offertes au niveau précédent (langage de programmation symbolique) mais il est maintenant établi que l’utilisation de GPUs est plus performante. Les GPUs sont des puces spéciales qui sont spécialisées dans le calcul numérique parallèle. Cette technologie a été introduite tout d’abord dans le contexte des jeux vidéos, pour le calcul 3D, mais a trouvé rapidement un usage dans les applications numériques d’apprentissage automatique. Les environnements de programmation spécialisés en AA (PyTorch et TensorFlow en sont de bons exemples) permettent à un programme écrit dans un langage symbolique (par exemple Python) de communiquer directement avec ce matériel spécialisé. Le même calcul, implémenté sur un CPU au lieu d’un GPU, serait beaucoup moins performant.
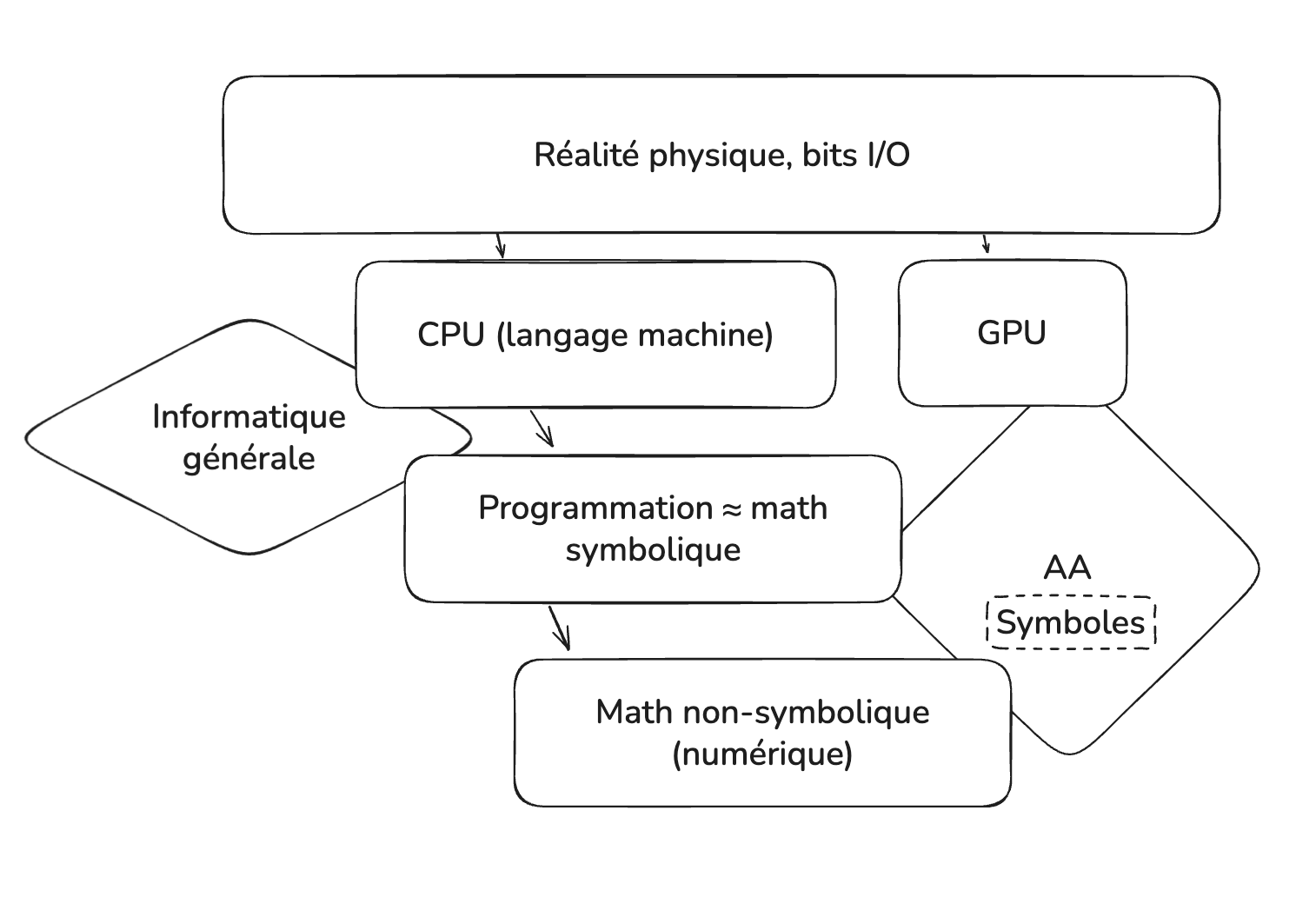
Retour vers les symboles#
On comprend mieux maintenant la distinction mentionnée souvent entre l’IA au sens classique, qui manipule des symboles, et l’apprentissage automatique, qui manipule plutôt des valeurs numériques, et dont on dit parfois qu’il est sub-symbolique. Dans un certain sens les deux manipulent des données qui sont ultimement des valeurs numériques (et même au final des entités physiques, les bits), mais il y a tout de même un sens clair à distinguer les deux types de mathématiques sur lesquels sont fondés l’IA classique et l’AA.
Les mots et leur sens#
Jusqu’ici, nous avons traité des données numériques ou tabulaires. Mais qu’en est-il du langage naturel ? Les mots portent du sens, mais pour un ordinateur ils doivent d’abord être convertis en nombres. Cette étape, qu’on appelle représentation vectorielle, est au cœur du traitement automatique du langage.
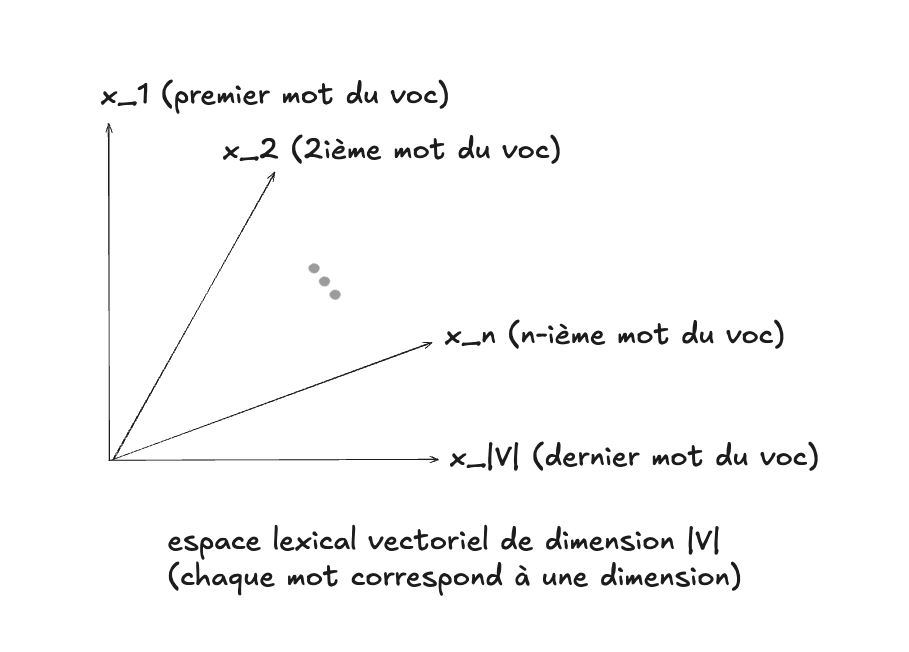
L’espace lexical vectoriel#
La manière la plus simple de représenter les mots est de construire un espace lexical où chaque mot du vocabulaire correspond à une dimension. Si le vocabulaire contient \(|V|\) mots, l’espace a \(|V|\) dimensions.
- Par exemple, si le vocabulaire est : {chat, chien, maison, arbre, voiture}, alors l’espace est à 5 dimensions.
- Le mot chat correspond à la première dimension, chien à la deuxième, etc.
Un mot peut alors être représenté comme un vecteur binaire, par exemple :
- chien → (0, 1, 0, 0, 0)
- maison → (0, 0, 1, 0, 0)
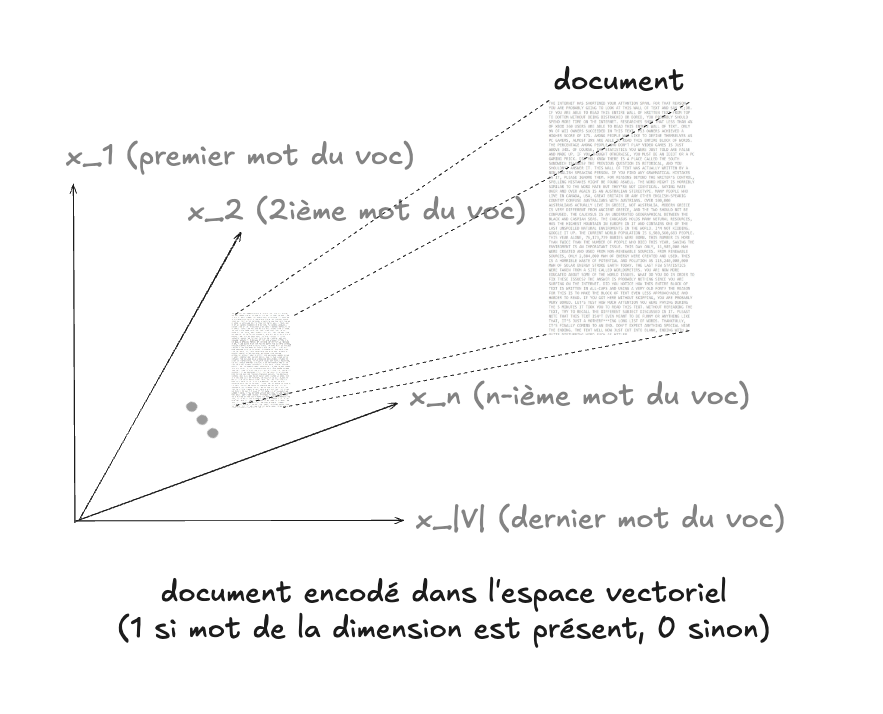
Encodage d’un document (sac de mots)#
Avec cette idée, on peut représenter un document entier en regardant quels mots du vocabulaire y apparaissent. On construit alors un vecteur binaire de longueur \(|V|\) :
- 1 si le mot est présent dans le document,
- 0 sinon.
Cette représentation est appelée sac de mots (bag of words), car on ne se préoccupe pas de l’ordre des mots ni de leur contexte, mais uniquement de leur présence/absence.
Exemple avec notre petit vocabulaire {chat, chien, maison, arbre, voiture} :
- Document : « le chat dort dans la maison »
- Vecteur : (1, 0, 1, 0, 0)
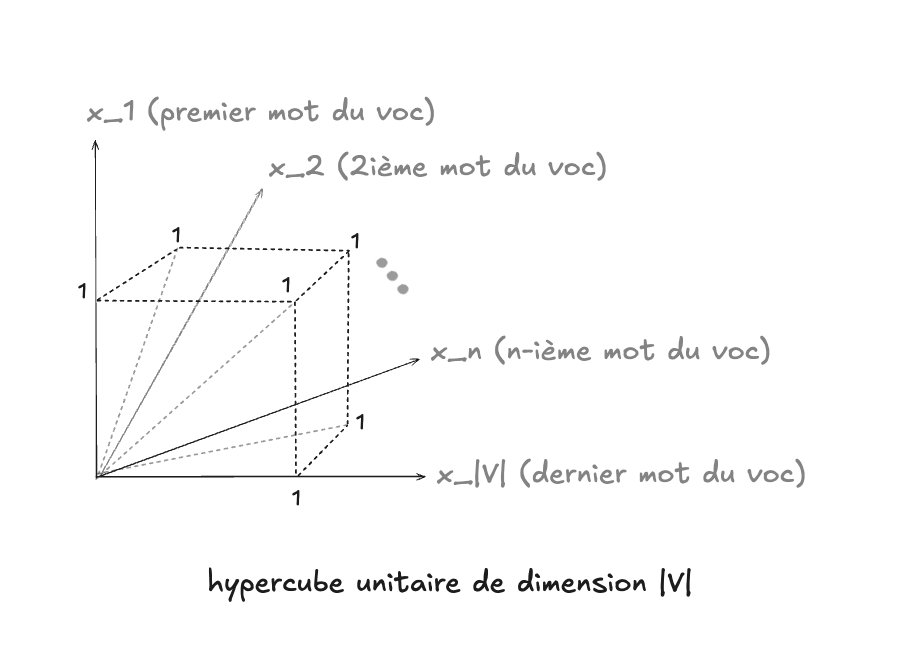
Si on visualise ces représentations, chaque document correspond à un point dans un hypercube unitaire de dimension \(|V|\). Chaque coordonnée vaut 0 ou 1.
- Le sommet (0, 0, 0, 0, 0) correspond à un document vide.
- Le sommet (1, 1, 1, 1, 1) correspond à un document qui contient tous les mots du vocabulaire.
- La distance entre deux vecteurs reflète une certaine similarité lexicale (par exemple, la distance de Hamming compte le nombre de mots différents).
Il n’est pas nécessaire de limiter la représentation des mots ou des documents à cet hypercube par contre. Il y a d’autres possibilités :
- Au lieu du critère binaire présence ou absence (0 ou 1), on pourrait utiliser le compte des mots (de 0 à $N$)
- On pourrait aussi utiliser un schéma de pondération plus sophistiqué comme TF-IDF, qui assigne une valeur aux mots proportionnelle à deux critères : (1) leur fréquence dans un document donné et (2) l’inverse de leur fréquence à travers la totalité des documents
Limites du sac de mots#
Malgré sa simplicité, cette approche a de sérieuses limites :
- Dimensionnalité énorme : le vocabulaire d’une langue peut contenir des dizaines de milliers de mots, ce qui rend l’espace vectoriel gigantesque.
- Vecteurs creux (sparse) : la plupart des documents n’utilisent qu’une fraction du vocabulaire, donc les vecteurs contiennent surtout des zéros.
- Pas de notion de sens : le sac de mots ne capture pas que chien et chiot sont liés, ou que banque peut avoir plusieurs sens.
- Pas de contexte : l’ordre des mots est perdu, alors que « le chien mord l’homme » et « l’homme mord le chien » devraient clairement avoir des sens différents.
Une manière simple avec laquelle on pourrait tenter d’atténuer le problème du
manque de contexte serait de considérer l’espace de toutes les suites possibles
de deux mots, par exemple. Nous allons explorer concrètement une
représentation de ce type (appelée bigramme) dans le travail noté du
quatrième module. Ceci ferait en
sorte d’ajouter un contexte aux mots : le bigramme livre intéressant serait
donc distinct du bigramme livre ennuyant. Le problème cependant serait que la
taille du “vocabulaire” augmenterait de manière dramatique : $|V|^2$ au lieu de
$|V|$, ce qui ferait également en sorte que la représentation serait encore plus
“creuse”.
Vers des représentations plus compactes : les plongements lexicaux#
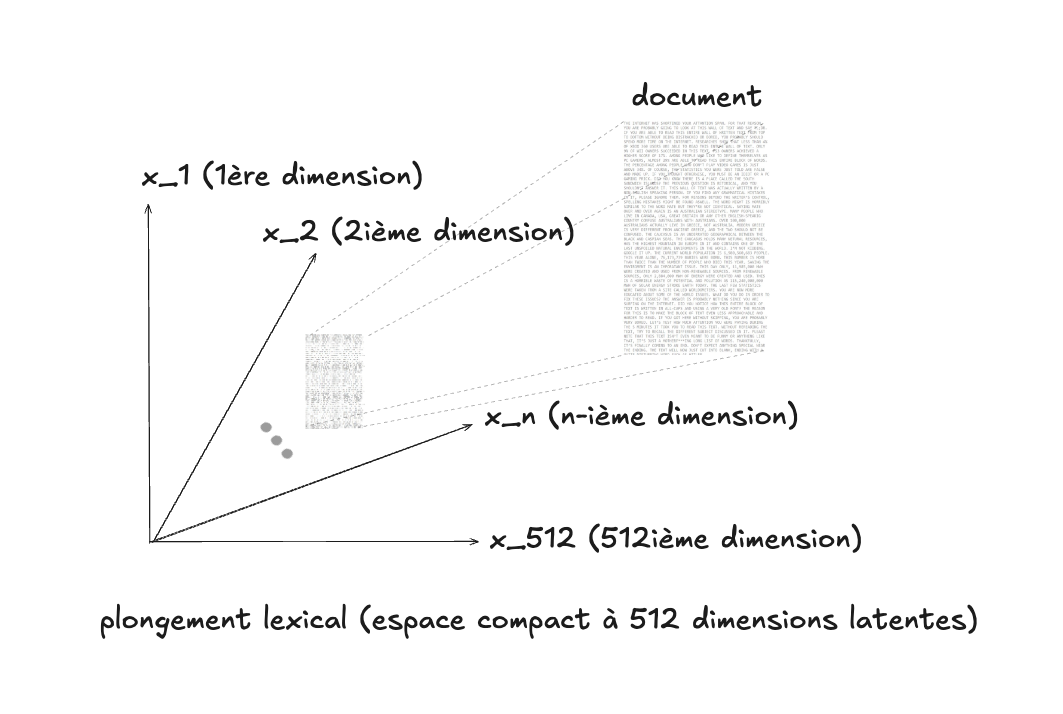
Pour dépasser ces limites, on utilise des représentations plus compactes et plus riches : les plongements lexicaux (word embeddings).
- Les mots ou documents sont projetés dans un espace de faible dimension (par exemple 100 ou 512).
- Les coordonnées ne sont plus 0 ou 1, mais des valeurs réelles continues.
- Ces coordonnées sont apprises automatiquement par un modèle sur de grandes quantités de textes.
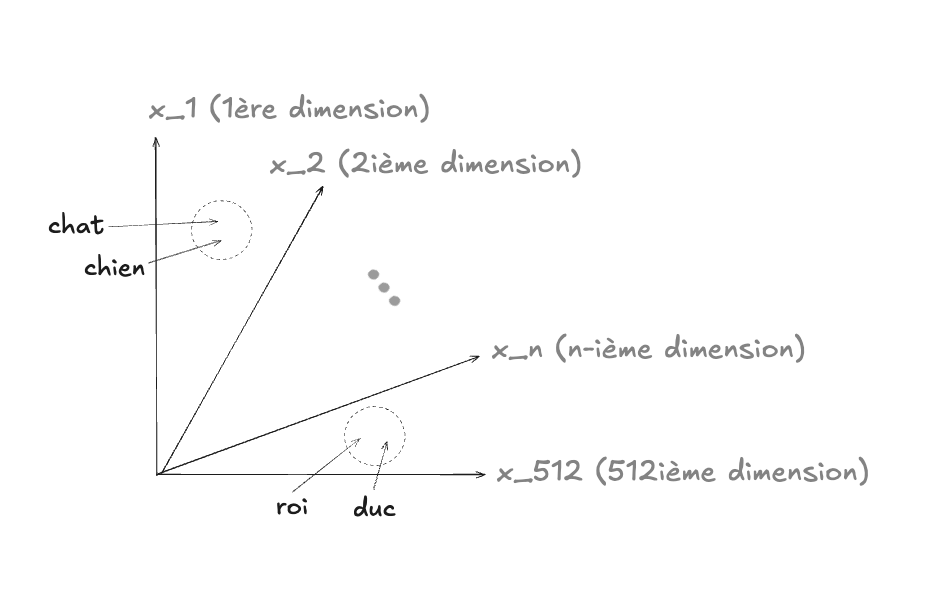
L’idée clé : deux mots qui apparaissent souvent dans des contextes similaires auront des vecteurs proches dans cet espace. Par exemple, roi et reine ou Paris et Londres.
Exemple intuitif#
Supposons qu’on entraîne un modèle sur un grand corpus. Il pourrait apprendre que :
- roi ≈ (0.51, 0.12, -0.34, …)
- reine ≈ (0.49, 0.18, -0.29, …)
- homme ≈ (0.44, 0.05, -0.21, …)
- femme ≈ (0.43, 0.09, -0.19, …)
La proximité vectorielle montre que roi est plus proche de reine que de voiture. Mieux encore, les différences de vecteurs permettent de capturer des analogies :
- roi - homme + femme ≈ reine
C’est cette capacité à capturer des relations sémantiques qui rend les plongements lexicaux si puissants.
Résumé#
- Espace lexical vectoriel : chaque mot correspond à une dimension.
- Sac de mots : un document est encodé comme un vecteur binaire (présence/absence).
- Hypercube unitaire : vision géométrique de tous les documents possibles.
- Limites : espace énorme, vecteurs creux, pas de contexte ni de sens.
- Plongements lexicaux : espaces compacts et continus où la proximité vectorielle reflète la proximité sémantique.
Ces représentations sont aujourd’hui la base du traitement du langage naturel, et elles alimentent directement les modèles modernes comme les réseaux de neurones récurrents, les Transformers et les grands modèles de langage.