Un scénario imaginaire, mais réaliste ! #

Imaginez une compagnie où il y a une chaîne de montage avec laquelle on assemble des téléviseurs.

Le problème #

Supposons que dans un endroit particulièrement délicat de la chaîne de montage, un problème avec un appareil d’assemblage particulier survienne parfois, que l’on aimerait détecter le plus rapidement possible.

Une solution possible #

On pourrait imaginer placer une caméra vidéo dont le but serait de visionner en permanence le flot des appareils en cours d’assemblage, pour tenter de détecter les problèmes. Pour ce faire, la caméra pourrait transmettre, à intervalles réguliers, les pixels de ce qu’elle capte, en tant que données à un modèle d’apprentissage automatique qui roulerait (en tant que programme) sur un serveur, pas très éloigné. Ce modèle convertirait les pixels de la caméra en tant que données numériques (les entrées, “inputs”), et effectuerait un calcul complexe sur ces valeurs, en vue de produire une valeur de sortie simple (“outputs”) : “oui, il y a un problème avec cette image”, ou “non, il n’y a pas de problème avec cette image” (ou encore, ce qui serait équivalent mais plus simple : “ok” ou “problème”). Cette valeur est binaire, dans le sens qu’elle a seulement deux valeurs possibles (peu importe lesquelles, en autant qu’il y en ait seulement deux). Sur la base de cette valeur binaire de sortie, on pourrait agir et envoyer un technicien, en cas de besoin, pour régler le problème.

Comment transformer une image en nombres? #

Transformer une image en une série de nombres n’est pas très compliqué. Il s’agit simplement de considérer la valeur des pixels formant une grille sur l’image, et transformer les couleurs en valeurs numériques (typiquement trois valeurs, correspondant à une combinaison précise de rouge, vert et bleu). Une image donnée sera donc transformée en une série de nombres réels.

Quelle est la nature de ce modèle? #

On parle ici d’un modèle au sens statistique du terme : une série de paramètres (des nombres, essentiellement) déterminant une fonction mathématique particulière. Il est important de comprendre qu’il ne s’agit pas d’un programme informatique au sens classique. Par analogie avec une fonction de base qu’on apprend au secondaire :

où $m$ et $b$ (les valeurs particulières qu’on leur donne) sont les paramètres qui déterminent cette fonction particulière. Dans un modèle d’apprentissage automatique, il y a beaucoup plus de paramètres, mais c’est essentiellement la même idée. Les paramètres d’un modèle sont donc essentiellement une série de nombres, rien de plus. Il est important à ce stade de bien comprendre la distinction entre ces deux séries de nombres dont nous parlons depuis le début :

• La série de nombres qui constituent les paramètres du modèle (aléatoires pour le moment, ils pourraient être n’importe quels nombres)
• La série de nombres qui proviennent des images que nous allons vouloir soumettre au modèle (correspondant à la couleur des pixels)

Nous allons faire en sorte qu’il y ait une interaction entre ces deux séries de nombres (en vue de produire une réponse binaire, soit seulement deux réponses possibles), et cette interaction constituera le modèle, en action.

Qu’est-ce que l’entraînement (ou l’apprentissage)? #

Notre but est maintenant de trouver une manière de calculer la valeur exacte de ces paramètres (nombres) pour notre modèle. Pour commencer, notre modèle a des valeurs aléatoires pour ses paramètres. Il est donc pratiquement impossible, à ce stade, que le modèle soit “bon”, dans le sens qu’il puisse fournir la bonne réponse dans un grand nombre de cas. Tout comme le sont ses paramètres à ce stade, sa performance est aléatoire, et est donc équivalente à un médecin qui tenterait de déterminer si un patient est malade en comptant seulement sur la chance, en tirant un dé par exemple, ou en consultant les astres. Pour que le modèle devienne bon, il faut trouver une manière de changer ses paramètres pour qu’il devienne plus performant, qu’il donne donc plus souvent une bonne réponse. C’est ce qu’on appelle l’apprentissage, et c’est dans ce sens que le modèle apprend.

Qu’est-ce qu’un ensemble de données d’entraînement? #

Nous avons tout d’abord besoin d’un ensemble de données d’entraînement, qui est constitué d’une série d’images (de téléviseurs en cours d’assemblage), prises au hasard, et accompagnées chacune d’une étiquette binaire (deux valeurs possibles : oui c'est un problème, ou non ce n'est pas un problème). Il est important de comprendre que la création d’un tel ensemble est souvent la partie difficile et coûteuse d’un projet d’apprentissage automatique, en vertu du fait que l’étiquette attachée à une image n’est pas donnée à priori. Il faut l’établir, ce qui constitue souvent un travail fastidieux et répétitif. Il est également nécessaire que cet ensemble d’entrainment soit représentatif de la réalité. Si les problèmes réels sont extrêmement rares, ils pourront être représentés comme tels dans l’ensemble d’entraînement, mais il est également possible de faire en sorte que la distribution des problèmes soit mieux balancée. Si on veut par exemple constituer un ensemble de 1000 images, il pourrait être composé de 500 cas problématiques, et 500 cas non-problématiques. De cette manière, même si les problèmes réels sont très rares (disons 1% des cas), la tâche du modèle sera plus facile car il aura de nombreux exemples de problèmes à analyser. Il sera plus à même de “comprendre” la nature des problèmes, car il en aura vu plus d’exemples lors de son entraînement. Il doit également être clair que toutes ces images seront très semblables, étant donné la très grande régularité du processus de la chaîne de montage. Mais il est raisonnable de supposer que les images de téléviseurs présentant un problèmes auront certaines différences visuelles. Le but sera de tenter la détection de problèmes en se basant sur ces différences, possiblement très subtiles.

Comment le modèle produit une réponse à partir d’une image? #

Le modèle produit une réponse (ou un diagnostic) en faisant essentiellement une opération mathématique (possiblement complexe) qui associe les nombres d’une image aux paramètres, en vue de produire un nombre binaire (la réponse). De manière pseudo-mathématique nous avons :

Notez ici que “image” est au singulier, car il s’agit d’une seule image, qui correspond par contre à plusieurs nombres, oui. La notation $F$ veut simplement signaler le fait qu’il s’agit d’une fonction au sens mathématique, soit un mécanisme qui fait l’association entre une ou plusieurs valeurs d’entrée, et une valeur de sortie.

Qu’est-ce que la fonction d’erreur? #

La fonction d’erreur détermine l’erreur moyenne qu’une version donnée du modèle (avec des valeurs précises pour les paramètres) entraîne. On ne doit pas confondre cette fonction avec le modèle lui-même, il s’agit d’une autre fonction, qui est reliée au modèle, mais qui n’est pas la même chose que le modèle. S’il y a 1000 images, dont 500 images “problème”, et 500 images “ok”, et que le modèle répond “ok” pour les 1000, alors il a fait 500 erreurs. On pourra donc dire que le modèle fait 50% d’erreur (500 erreurs divisée par la taille de l’ensemble, 1000). Un peu plus mathématiquement, on peut considérer que l’erreur est une fonction des données d’entraînement et des paramètres (en d’autres termes, les “inputs” de la fonction) et que la valeur de cette fonction est simplement le ratio entre le nombre d’erreurs produites avec ces données et ces paramètres particuliers (le numérateur) et la taille des données (le dénominateur) :

Notez ici que “images” est au pluriel, car il s’agit de toutes les images de l’ensemble d’entraînement. La fonction d’erreur calcule une moyenne sur l’ensemble des images de l’ensemble d’entraînement.

Qu’est-ce que l’entraînement (ou l’optimisation de la fonction d’erreur)? #

La partie cruciale est ici : on aimerait une procédure qui va changer la valeur des paramètres (qui au départ sont des valeurs aléatoires) de manière à réduire l’erreur, idéalement l’amener à zéro. Parfois il est possible de trouver les bonnes valeurs pour les paramètres “d’un coup”, mais plus souvent, il est plus pratique de le faire progressivement. La valeur de la fonction d’erreur va donc diminuer graduellement, de manière itérative, à mesure que nous allons modifier les paramètres, la fonction d’erreur va donc être “optimisée”.

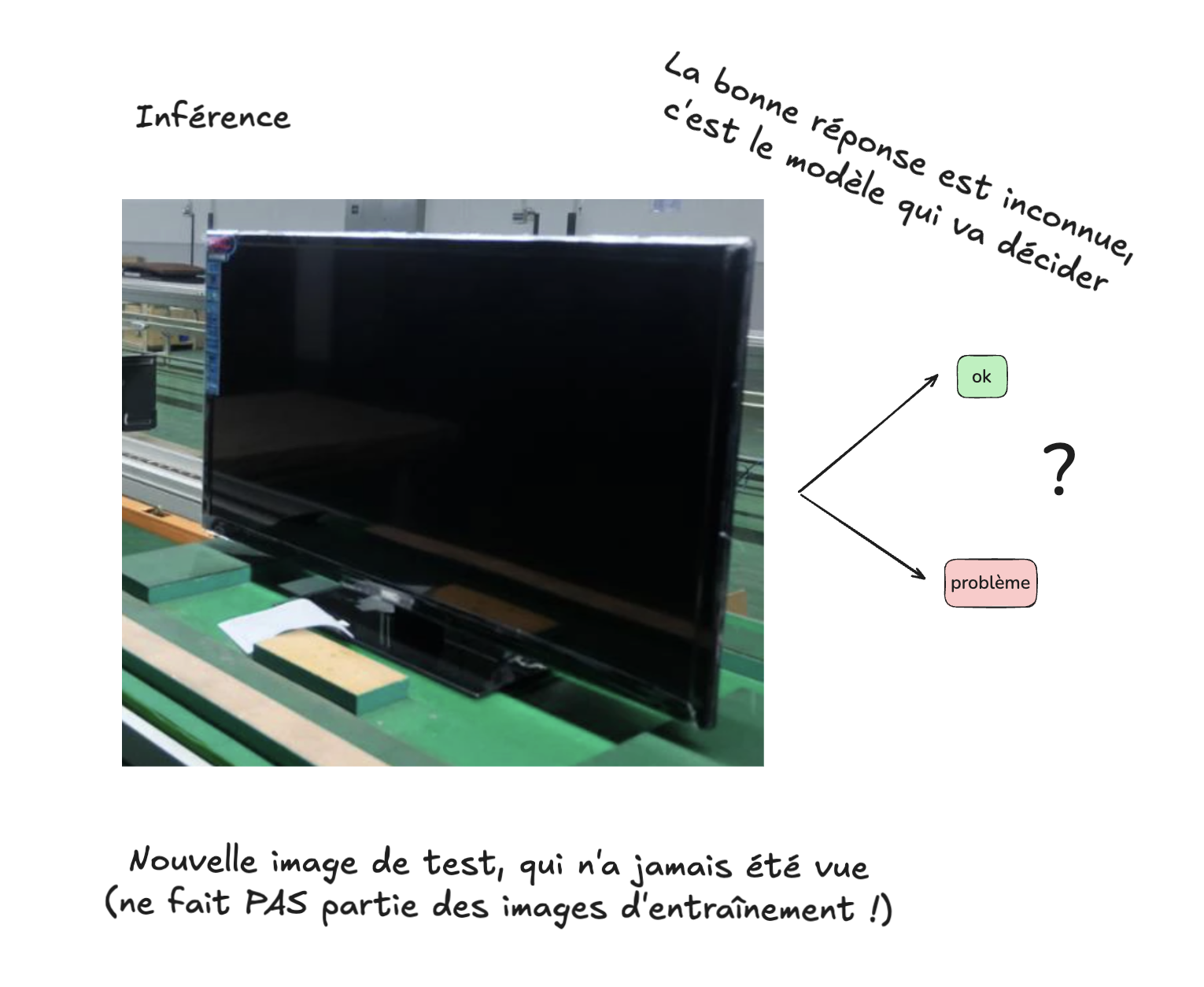
Qu’est-ce que l’inférence (ou l’utilisation du modèle dans la réalité)? #

Une fois les bonnes valeurs pour les paramètres trouvées, la tâche est accomplie, le modèle est enfin prêt à être utilisé dans une opération réelle. On conserve donc précieusement les valeurs de ces paramètres, et on les place dans une version “officielle” du modèle, qui devra traiter des données provenant de la chaîne de montage, en production. Ces données seront “nouvelles”, dans le sens qu’elles n’ont pas servies à l’entraînement du modèle (elles ne feront nécessairement pas partie de l’ensemble des 1000 images d’entraînement). Mais notre espoir est que le modèle aura appris à “généraliser”, à partir des exemples qu’il aura vus pendant son entraînement. Si jamais le modèle ou la couleur des téléviseurs changent (donc la couleur des pixels que la caméra va en capter), il est possible que notre modèle se comporte moins bien, et fasse donc plus d’erreurs. Il sera donc peut-être nécessaire de procéder à son ré-entraînement.

En quoi est-ce que ceci constitue de l’intelligence? #

Une question valide qui peut persister après cette expérience de pensée est la suivante : en quoi peut-on dire que ceci constitue un mécanisme doté d’intelligence? Les débats à ce sujet ne manquent pas, depuis longtemps, mais en général on tend à reconnaître que les tâches qui nécessitent la perception humaine (dans ce scénario, la vision) sont difficiles pour les ordinateurs et la programmation au sens classique. Cette idée se nomme le Paradoxe de Moravec. Étant donné cette difficulté fondamentale, on a tendance à considérer qu’un programme informatique qui repose sur un mécanisme de perception (comme dans cet exemple) est intelligent, tandis qu’un programme qui effectue des opérations mathématiques courantes (par exemple Excel), ne l’est pas. On sent bien ici qu’il s’agit d’un problème profond de catégories, avec lequel on se rapproche de la philosophie.