Classification naïve bayésienne pour détecter les pourriels (travail noté 2) #

La classification naïve bayésienne est un algorithme d’apprentissage supervisé qui fonctionne avec les probabilités. Nous avons vu deux variantes de cet algorithme :

1. La classification de simples points en 2d avec un modèle gaussien
2. La classification de vecteurs en haute dimension avec un modèle multinomial

Un problème classique qui peut être traité avec cet algorithme est la classification de courriels. On peut tenter d’estimer la probabilité qu’un courriel soit en fait un pourriel en prenant en compte les mots particuliers qu’il contient, l’idée étant que certains mots auront tendance à être plus souvent utilisés selon qu’il s’agit d’un pourriel ou d’un courriel.

Comme nous l’avons vu, la classification naive bayésienne est un algorithme d’apprentissage génératif, ce qui veut donc dire qu’on considère tout d’abord deux modèles (un pour chaque classe, pourriel ou courriel) qui sont en charge de générer les données qu’on observe (plutôt que de directement les classifier) :

ou encore, de manière plus compacte :

Mais étant donné que ce qui nous intéresse, dans ce contexte, est de classifier les courriels, nous utilisons le théorème de Bayes pour “inverser” les modèles, pour ainsi obtenir une règle de classification simple (qui prédit la classe plutôt que les mots):

Consignes #

1. Suivez les instructions qui suivent pour construire tout d’abord le fichier Google Sheets avec toutes les données nécessaires.

2. Une fois qu’il est complété et fonctionnel, partagez votre fichier et copier le lien vers celui-ci dans un document PDF (Attention : aucun autre format que PDF ne sera accepté).

3. Répondez aux questions d’interprétation de la dernière section dans le même fichier PDF, en fournissant des réponses claires et précises.

Entraînement du modèle #

Voyons comment il est possible de calculer ces probabilités en entraînant un modèle de classification sur une série de courriels particuliers.

Étant donné que nous allons utiliser le tableur en ligne Google Sheets, assurez-vous tout d’abord qu’il est correctement configuré.

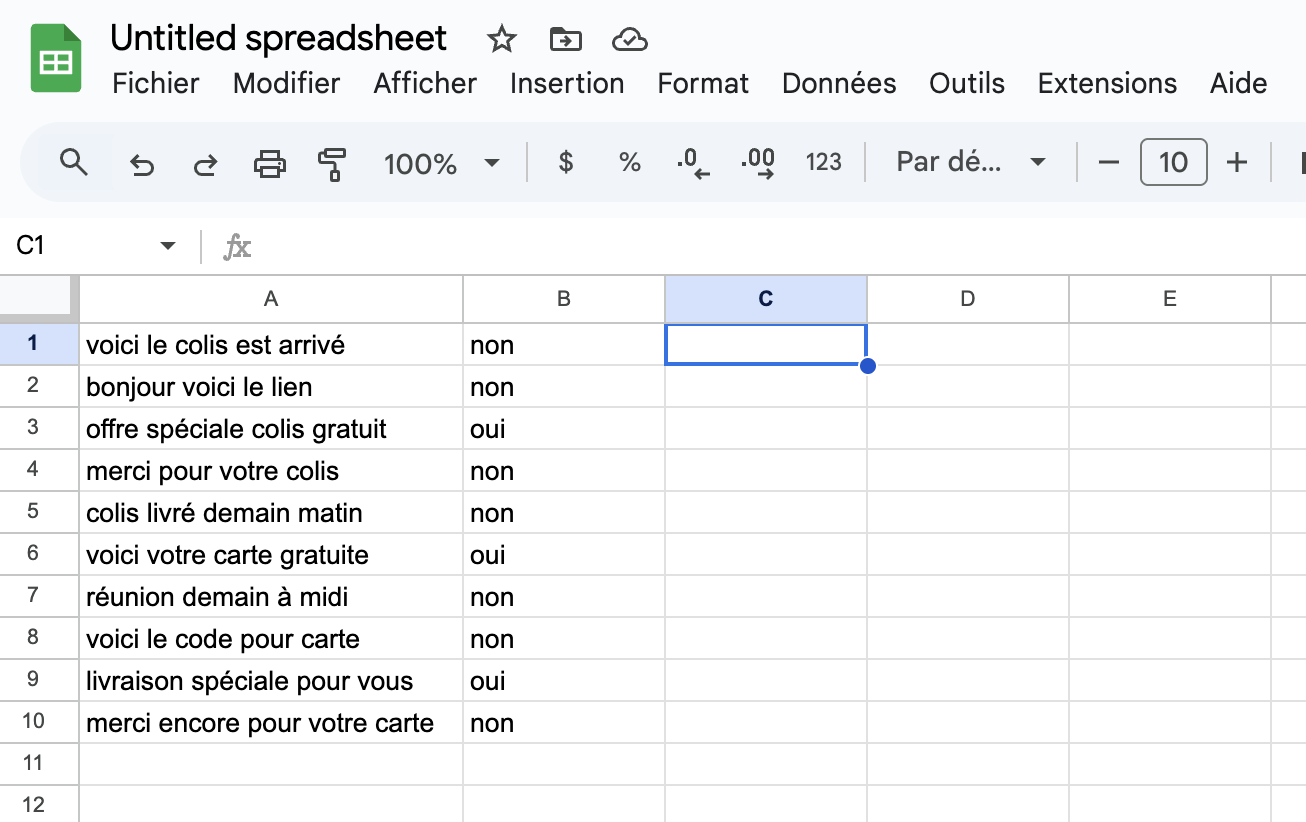
Copiez tout d’abord ces 10 mini-courriels dans la colonne A d’une nouvelle “feuille” Google Sheets, un courriel par rangée (assurez-vous d’utiliser correctement la fonction “copier-coller”, si vous le faites) :

voici le colis est arrivé
bonjour voici le lien
offre spéciale colis gratuit
merci pour votre colis
colis livré demain matin
voici votre carte gratuite
réunion demain à midi
voici le code pour carte
livraison spéciale pour vous
merci encore pour votre carte

Pour avoir un aperçu de la tâche d’étiquetage des données (qui dans un scénario réel peut s’avérer très coûteuse et laborieuse), vous êtes invités à tenter tout d’abord de catégoriser vous-mêmes les courriels dans la colonne B, en utilisant la valeur oui si vous considérez qu’il s’agit d’un pourriel, ou non (ce n’est pas un pourriel) sinon.

Si vous n’avez pas envie de vous soumettre à cet exercice à ce stade, vous pouvez toujours copier ces valeurs (dans la colonne B) :

non
non
oui
non
non
oui
non
non
oui
non

À ce stade, votre feuille devrait ressembler à ceci :

Calculons tout d’abord dans la colonne C la probabilité à priori qu’un courriel quelconque soit un pourriel ou non (sans prendre en considérations les mots donc, pour le moment) :

=MAP(UNIQUE(B1:B10), LAMBDA(x, COUNTIF(B1:B10, x) / COUNTA(B1:B10)))

Si vous obtenez une erreur avec la formule à ce stade, il est très possible que les paramètres linguistiques de votre Google Sheets ne soient pas correctement configurés.

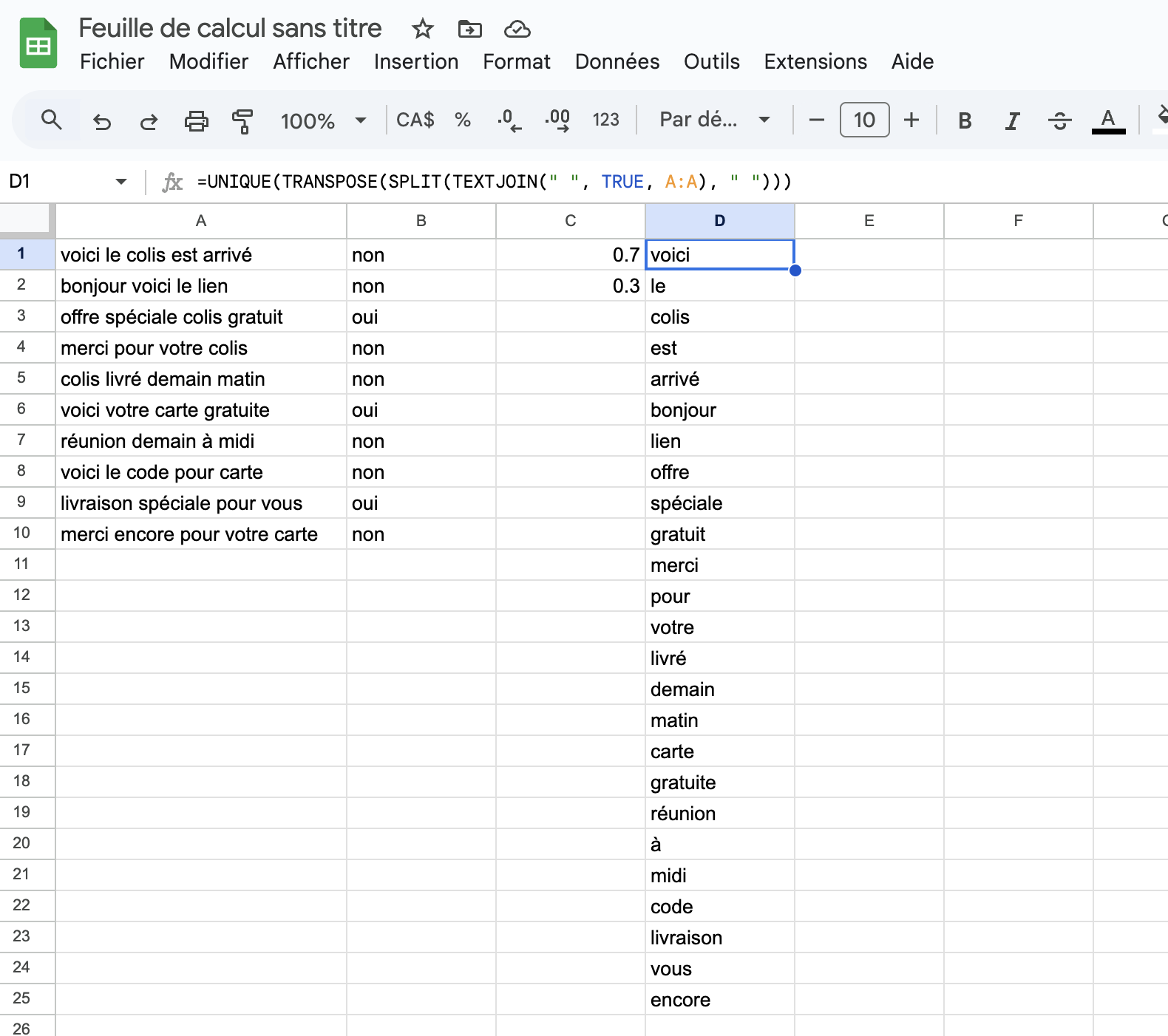
Ces probabilités à priori nous serviront plus loin. Définissez ensuite la colonne D avec cette formule :

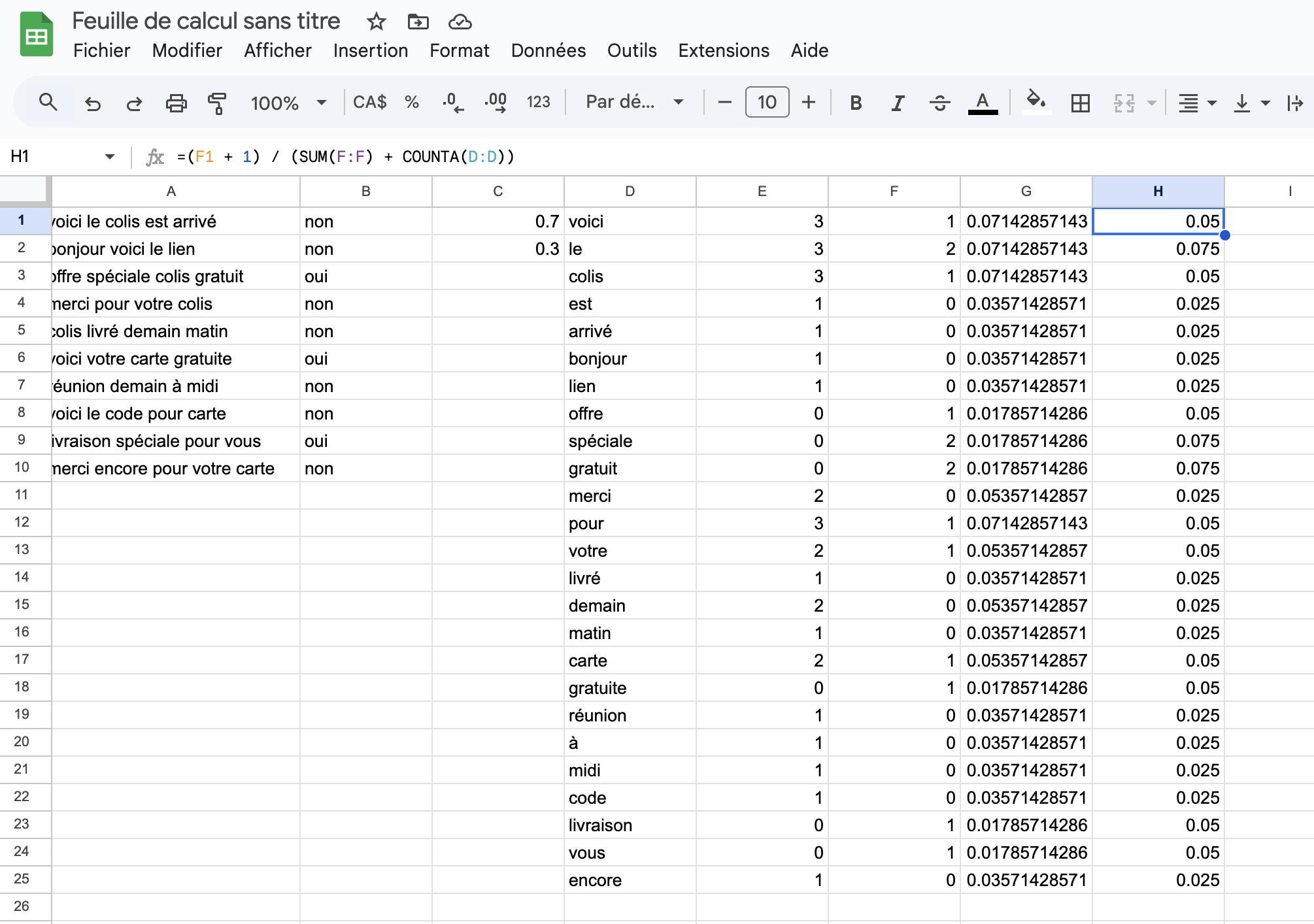
=UNIQUE(TRANSPOSE(SPLIT(TEXTJOIN(" ", TRUE, A:A), " ")))

La colonne D devrait maintenant contenir le vocabulaire des courriels :

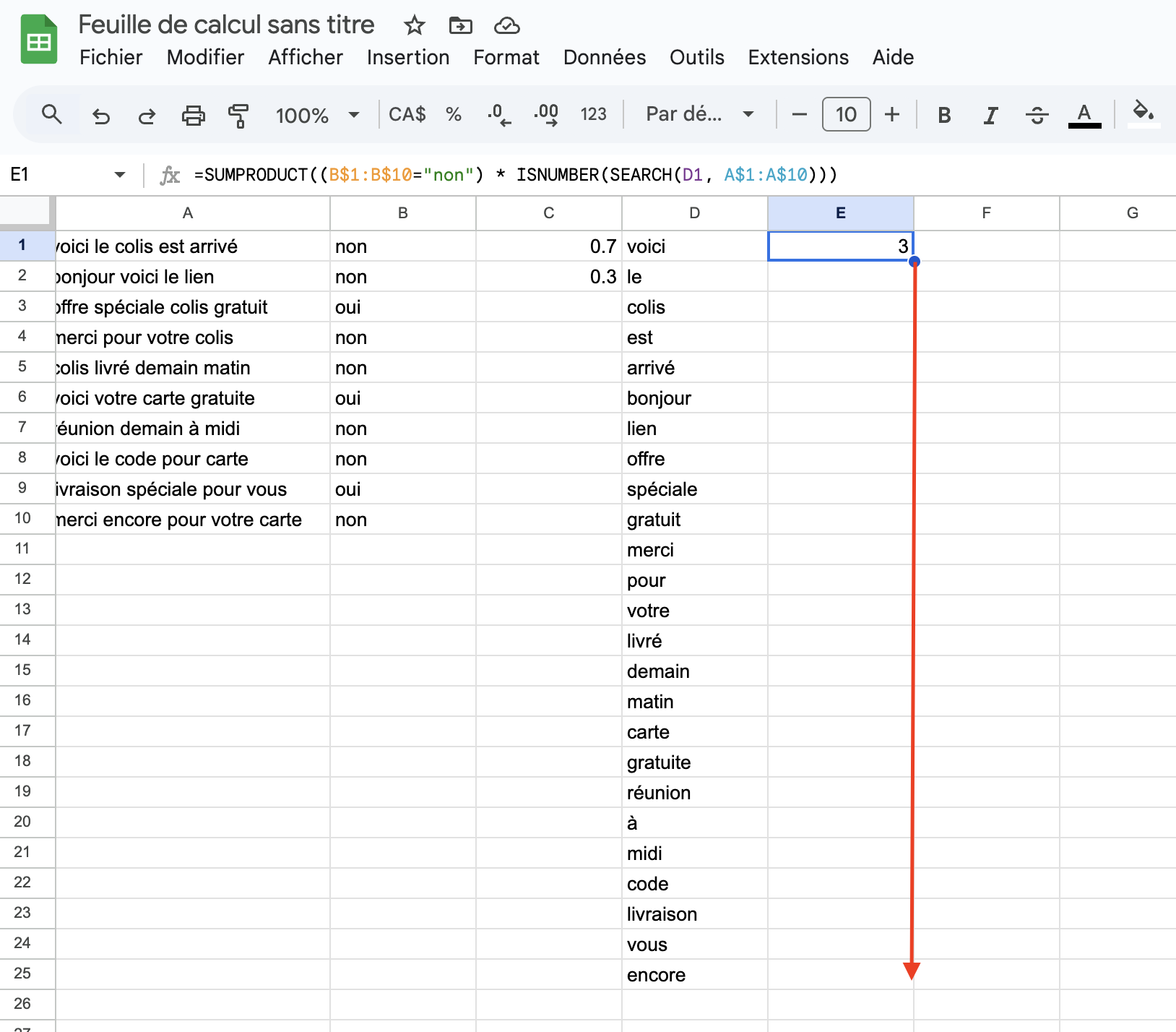
La colonne E devrait ensuite correspondre au nombre de fois où les mots de la colonne D apparaissent dans les courriels valides (qui donc non, ne sont pas des pourriels) :

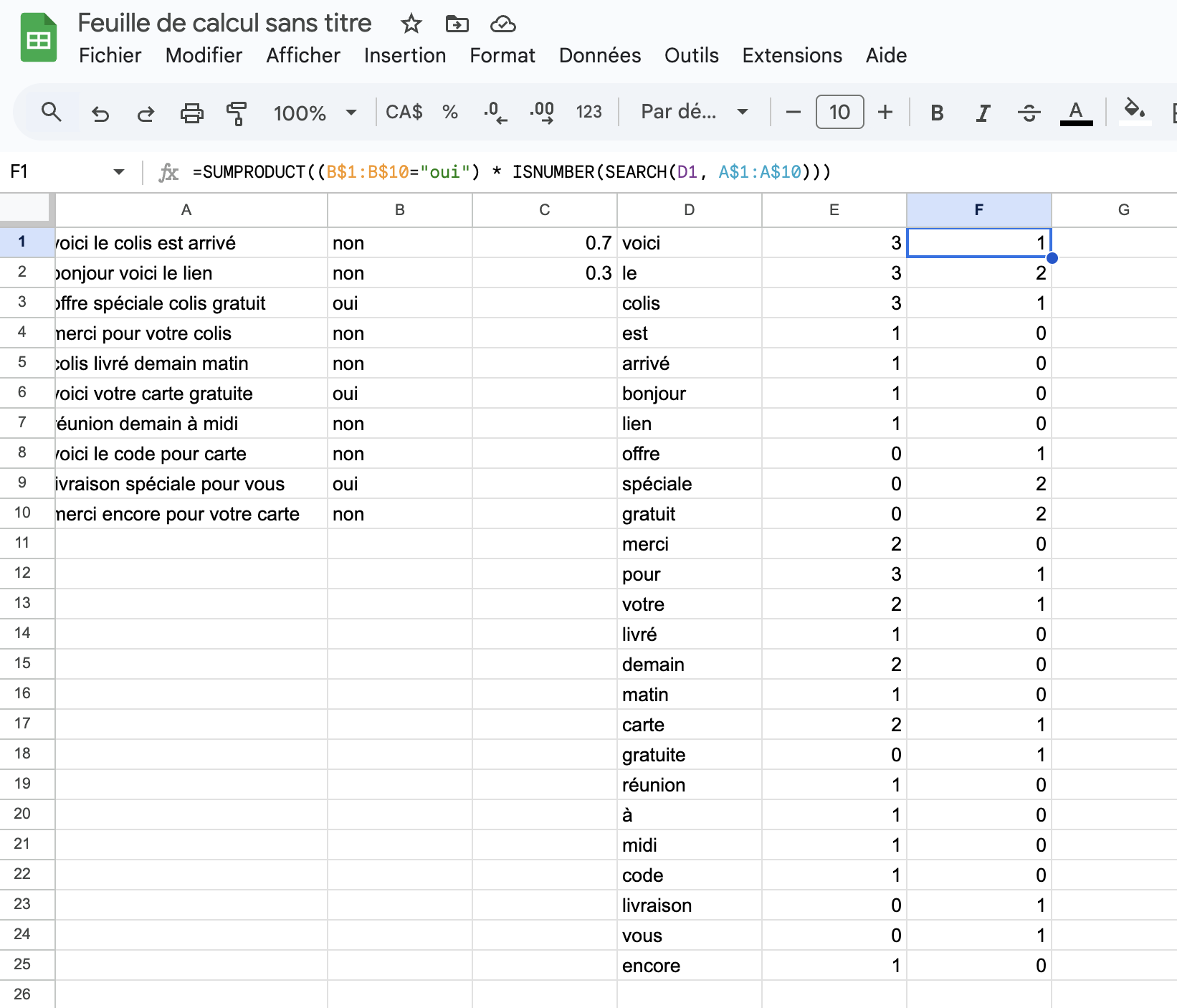
=SUMPRODUCT((B$1:B$10=`non`) * ISNUMBER(SEARCH(D1, A$1:A$10)))

et de manière similaire pour la colonne F et la fréquence des mots qui apparaissent dans les courriels qui oui, sont des pourriels :

=SUMPRODUCT((B$1:B$10=`oui`) * ISNUMBER(SEARCH(D1, A$1:A$10)))

Notez que les colonnes E et F doivent avoir le même nombre d’éléments que la colonne D (il faut donc utiliser la fonction de remplissage automatique, pour laquelle le plus simple est de soit glisser (drag) la première cellule vers le bas, une fois qu’elle a été calculée, ou encore de double-cliquer sur le petit “+” noir qui apparaît en bas à droite de la première cellule).

À partir de ces fréquences de mots pour chaque classe (oui ou non), on peut maintenant calculer la probabilité conditionnelle de chaque mot du vocabulaire, étant donné le fait qu’un courriel soit oui ou non un pourriel. Donc la colonne G correspond à la probabilité des mots étant donné que non il ne s’agit pas d’un pourriel :

=(E1 + 1) / (SUM(E:E) + COUNTA(D:D))

et de manière similaire la colonne H est la probabilité des mots quand on sait que oui il s’agit d’un pourriel :

=(F1 + 1) / (SUM(F:F) + COUNTA(D:D))

Encore une fois les colonnes G et H doivent avoir la même taille que celle du vocabulaire (colonne D), il faut donc s’assurer d’utiliser le mécanisme du remplissage automatique décrit précédemment.

Notre modèle est maintenant entièrement entraîné, et il est donc prêt pour son utilisation!

Utilisation du modèle (inférence) #

Nous allons maintenant utiliser le modèle pour déterminer si un nouveau courriel (qui n’a pas servi à l’entraînement) est un pourriel ou non. Dans la colonne I entrez un courriel à tester :

voici votre carte spéciale

Faites l’extraction des mots du courriel dans la colonne J :

=TRANSPOSE(SPLIT(I1, " "))

Nous avons maintenant besoin, dans la colonne K, de la probabilité des mots de ce courriel de test dans l’hypothèse où non, ça ne serait pas un pourriel :

=IFERROR(XLOOKUP(J1, D:D, G:G), 1E-5)

et de manière similaire pour la colonne L, avec la probabilité des mots du courriel dans l’hypothèse où oui il s’agit d’un pourriel :

=IFERROR(XLOOKUP(J1, D:D, H:H), 1E-5)

Les colonnes K et L doivent avoir la même taille que la colonne J, donc assurez-vous d’utiliser le remplissage automatique. Calculons dans la colonne M la probabilité que non le courriel n’est pas un pourriel :

=PRODUCT(K:K) * C1

Et dans la colonne N la probabilité que oui le courriel est un pourriel :

=PRODUCT(L:L) * C2

Notre classification finale sera dans la colonne O :

=IF(M1 > N1; "non"; "oui")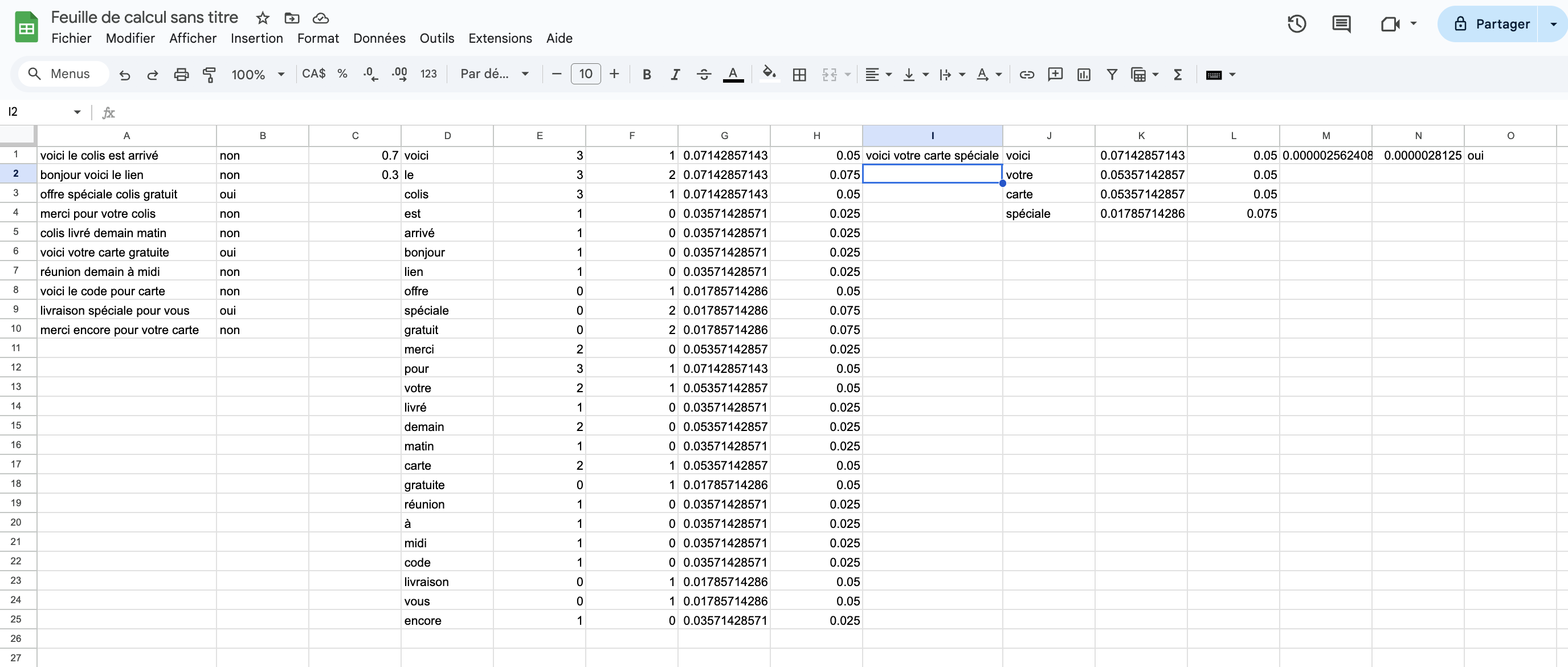

Questions d’interprétation #

1. Que se passe-t-il si vous changez le mot “spéciale” par le mot “livrée” dans le courriel de test de la cellule I1?

2. Après ce changement, expliquez les probabilités qu’on retrouve aux cellules K4 et L4 associées au nouveau mot “livrée”. D’où proviennent ces nouvelles valeurs, et pourquoi a-t-on besoin d’avoir recours à celles-ci dans le cadre du calcul?

3. Est-ce que ce modèle est paramétrique ou non? Expliquez pourquoi.

4. S’il s’agit d’un modèle paramétrique, quels sont les paramètres du modèle (quelles colonnes)?

5. Quelles colonnes constituent la partie générative du modèle? Expliquez pourquoi.

6. Quelles colonnes constituent la partie discriminative du modèle? Expliquez pourquoi.

7. Quelle est la signification des nombres dans les cellules G11 et H11, comment peut-on les interpréter?

8. Quelles sont les probabilités non-conditionnelles (à priori)? À quoi servent-elles?

9. Est-ce qu’il serait possible d’utiliser seulement ces probabilités non-conditionnelles pour faire un modèle de classification? Quelles conséquences ça entraînerait?

10. De quelle manière peut-t-on dire que ce modèle généralise?

11. Est-ce que l’ordre des mots joue un rôle dans les décisions de ce modèle? Expliquez pourquoi c’est ainsi.

12. Si l’ordre des mots ne joue pas de rôle, comment pourrait-on modifier le modèle de manière à ce qu’il en joue un?

13. Est-ce que certains mots aident particulièrement le modèle? Si oui pourquoi?

14. Est-ce que certains mots sont moins utiles? Si oui pourquoi?