Apprivoisez un réseau de neurones (travail noté 3) #

Voici l’application Tensorflow Playground, offerte en logiciel libre, que nous avons quelque peu adaptée pour les besoins de ce cours. Elle permet d’explorer de manière interactive et intuitive le fonctionnement des réseaux de neurones.

Consignes #

En utilisant l’application interactive, effectuez les expériences proposées dans la section “Instructions et questions” ci-bas.
Répondez de manière claire et précise aux questions d’interprétation dans un fichier PDF (Attention : aucun autre format que PDF ne sera accepté).

Instructions et questions d’interprétation #

En vous assurant tout d’abord que le “type de problème” (menu déroulant à droite) est la “classification”, considérez les 4 jeux de données proposés.
Des 4 jeux de données proposés, lequel vous apparaît ensuite le plus facile à classifier (en deux classes distinctes, orange et bleue), pour un algorithme d’apprentissage automatique (pas seulement un réseau de neurones)? Expliquez pourquoi.
Considérez maintenant le jeu de données avec lequel deux petits groupes de points sont disposés en diagonale, l’un par rapport à l’autre.
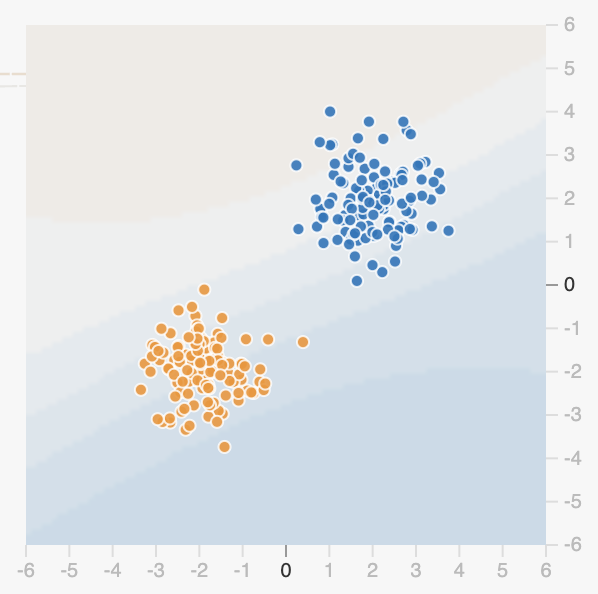
Assurez-vous de n’avoir aucune couche cachée, et seulement les caractéristiques $X_1$ et $X_2$ activées. Quelle est l’erreur (ou perte) d’entraînement? Appuyez plusieurs fois sur le bouton de rafraîchissement, et constatez les variations au niveau de cette initiale (avant tout entraînement):
Que signifient ces erreurs et ces variations (pourquoi l’erreur initiale est parfois plus haute, et parfois plus basse), et de quelle manière peut-on les constater visuellement?
Quelle est la différence entre ce problème de classification et celui que nous avons vu dans le deuxième module avec la régression logistique?
Ajustez maintenant la valeur de “bruit” à 25, et appuyez sur le bouton “régénérez” à quelques reprises. Est-ce que ceci rend la tâche de classification plus facile ou plus difficile pour un algorithme d’apprentissage? Expliquez pourquoi.
Remettez le “bruit” à 0, et choisissez maintenant ce jeu de données :
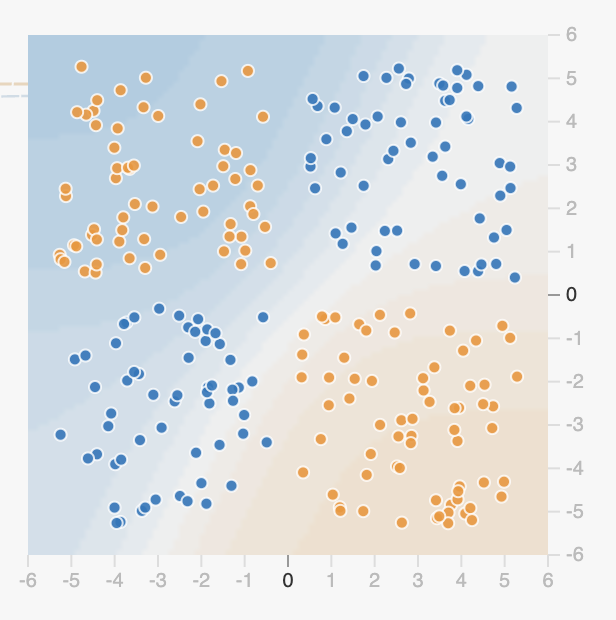
À priori, est-ce qu’il vous apparaît possible qu’un modèle ayant servi à classifier le précédent jeu de donnes puisse servir à classifier celui-ci? Expliquez pourquoi. Tentez l’expérience, que se passe-t-il?
Ajoutez maintenant une couche cachée avec trois neurones, quel est l’effet sur l’entraînement? N’oubliez pas que la fonction d’entraînement est démarrée en appuyant sur ce bouton :
Ajoutez maintenant une deuxième couche cachée avec deux neurones cette fois. Effectuez quelques entraînements, en n’oubliant pas d’utiliser la fonction de rafraîchissement entre les entraînements (pour faire en sorte que les paramètres initiaux puissent varier). Qu’observez-vous, et que pouvez-vous en conclure?
Une fois qu’un entraînement a atteint un certain niveau d’erreur (assez bas, probablement, si l’entraînement a bien fonctionné), est-ce que le fait de le laisser continuer pendant une longue période (et donc d’atteindre un très grand nombre d’époques) fait une différence? Comment expliquez-vous cela? Quel mot pourrait-on utiliser pour illustrer ce phénomène particulier?
Comment expliquez-vous le fait que l’entraînement ne converge pas toujours vers la même solution, et par extension, la même valeur d’erreur?
Enlevez maintenant toutes les couches cachées, et ne laissez activée que la caractéristique $X_1X_2$. En entraînant le modèle à plusieurs reprises avec cette configuration, qu’observez-vous, et comment l’expliquez-vous?
Considérez maintenant ce troisième jeu de données :
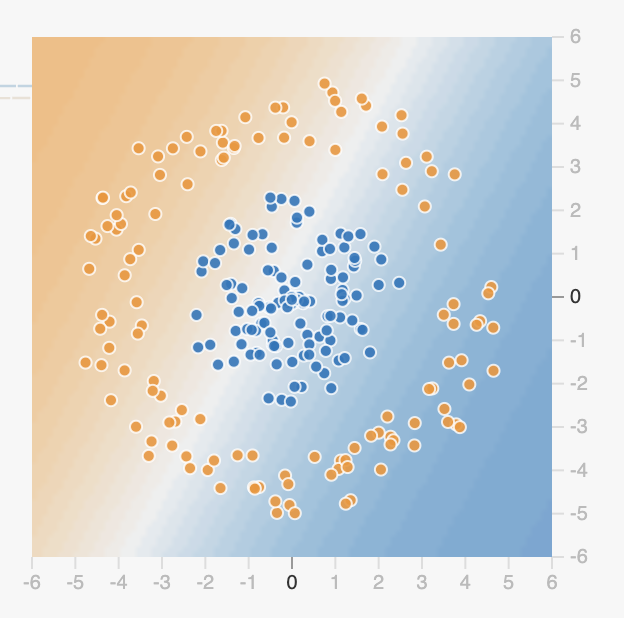
Sans aucune cachée, et seulement les caractéristiques $X_1$ et $X_2$ activées, est-ce qu’il est possible de résoudre ce problème?
Est-ce que la situation change en remplaçant les caractéristiques $X_1$ et $X_2$ par les caractéristiques $X_1^2$ et $X_2^2$? Comment peut-on expliquer cela? Indice : considérez l’équation du cercle.
En remettant seulement les caractéristiques $X_1$ et $X_2$, est-ce qu’il est possible de réduire l’erreur à l’aide de couches cachées?